418 419

4 | 8    Programowanie dynamiczne

Graf rozpatrywanego procesu przedstawiono na rys. 9.6.

Rysunek 9.6

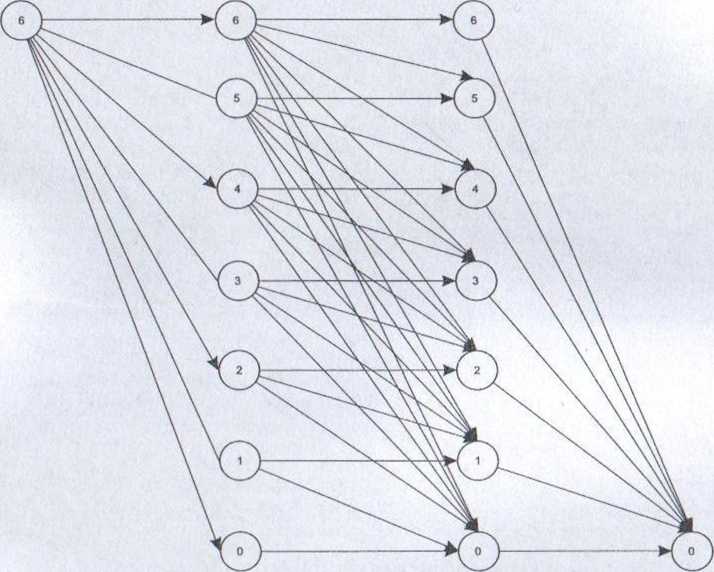
Zajmiemy się teraz rozwiązaniem zadania, zapisując i rozwiązując kolejne równania optymalności.

Etap 3

Przypuśćmy, że na początku etapu 3 rozpatrywany proces znalazł się w stanie y .i^e Z.i-

Obliczamy wartość:

gtCy₃) = max l/iO’3. -*3): ^eX,(y₃)),

czyli maksymalny dochód uzyskany przy realizacji projektu ITI, jeżeli na jego realizację przydzielono środki w wysokości y₃ jednostek. Obliczamy kolejno:

*J(0)=/₃(0,0) = 0,    xf(0) = 0,

gt(l)=/t(l. 1) = 2,8,    aJ(1)=1,

g?(2) =6 (2, 2) = 4,5,    a?(2) = 2,

gf(3)=6(3, 3) = 6,5,    a?(3) = 3,

gt (4) =6(4, 4) = 7,8,    Af(4) = 4,

«f(5) =/₃(5, 5) = 9,0,    Af<5)=5,

gf (6) =/, (6. 6) = 10,2,    a* (6) = 6.

Etap 2

Przypuśćmy, że na początku drugiego etapu proces znalazł się w stanieje Y₂. Chcemy ustalić, jakie środki należy przydzielić na realizację projektu 11 w zaistniałej sytuacji, zakładając, że do końca procesu będziemy postępowali w sposób optymalny. W tym celu obliczamy wartość

gf(y₂) = max {/,(y₂, x₂) +g^(y₂-x₂): x₂eX₂(y₂)\,

czyli maksymalny zysk z realizacji projektów o numerach 2 i 3, jeżeli na ich realizację możemy przydzielić łącznie środki w wysokości y₂. Dla kolejnych stanów dopuszczalnych obliczamy:

gf(0) = 0 oraz a?(0) = 0,

g?(]) = max<	6(1, 0)+g?(D 6(1, l)+«?(0)	= max <	0 + 2,8 2,5 + 0	► = max |
oraz jrf (1) = 0,
gf(2) = max	6(2, 0) + gf(2) 6(2, l) + gf(D 6(2, 2) + g?(0)	i • = max	0 +4,5 2,5+ 2,8 4,1+0	► = max «

2,8

2.5

4,5

5.3

4.4

oraz a$(2) = 1,

= 2,8

> = 5,3

6(4, 3) + gf(l)

	0 +6.5'		6,5
■ = max •	2,5+ 4,5 4,1+2,8	= rnax <	li
	5,5 + 0		5,5
	0 +7,8		7,8
	2,5 + 6,5		9
> = max	4,1 +4,5	■ = max <	8,6
	5,5 + 2,8		8,3
	6,5+0		6,5

gf (3) = max

6(3, 0) + g*(3) 6(3, l) + g*(2) 16(3, 2) + g*(l) 6(3, 3) + g$(0)

oraz x* (3) = 1,

6(4, 0) + gf(4) 6(4, D + *!(3)

gf (4) = max ■ oraz xf (4) = 1,