523 2

Soczewka w powietrzu niech będzie naszym przykładem sumowania zdolności skupiających Jeśli soczewka jest w powietrzu, to    I. oznaczmy też

nJ ■ n₂■ n. Czytelnik zechce sam wyprowadzić wzór na zdolność skupiają: jeśli będzie pamiętał o podstawieniu wielkości zredukowanych, to otrzyma warnik w postaci:

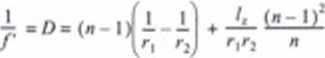
a dla soczewki cienkiej, gdy I, = 0:

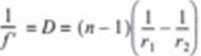
Śledząc załamanie promienia na powierzchni sferycznej otrzymaliśmy zależność (16.3) między odległościami przedmiotu i obrazu od pow ierzchni załamującej a jej ogniskowy mierzoną w powietrzu. Jeśli układ optyczny umieszczony jest w powietrzu. to współczynnik załamania przed i za układem równy jest jedności i w takim przypadku zależność (16.5) matowy zapisać:

Przypomnijmy. Ze każdemu położeniu przedmiotu odpowiada jedno określone połoZeme obrazu, a o zależności między tymi położeniami decyduje ogniskowa. Matematycznie formułują to wzory (16.5) i (16.11). Jeśli więc wyobrazimy sobie układ optyczny z ekranem umieszczonym za nim w stałej odległości, to ..ostry" obraz na ekranie otrzymamy tylko dla jednej odległości przedmiotu. Chcąc otrzymać ostry obraz, przedmiotu umieszczonego w innej odległości, muumy zmienić odległość między układem a ekranem Musimy'¹ Nie. można tez odpowiednio zmienić ogniskową układu. Tak właściwie jest w oku! Odległość między ekranem (siatkówką) a układem optycznym jest stała, mimo to oglądamy przedmioty bliskie i dalekie ostro, ponieważ soczewka oczna akomoduje zmieniając swą ogniskową przez zmianę promieni krzywizny. Obraz rzeczywisty przedmiotu położonego błiżej obserwatora zawsze jest większy od obrazu lego przedmiotu położonego dalej. A jak to jest w oku przy zmieniającej się ogniskowej? Obra/ leż jest większy, choć w innym stopniu. Miarą pcn%i{ktzfma liniowego P jcst stosunek l'/i W oku. jeśli np. s maleje przy stałym s\ to powiększenie rośnie, choć ..słabiej" niż w przypadku stałej ogniskowej.

16.2.2. Aberracje układu optycznego

Dotychczas omaw iając układ optyczny, choć może usilnie tego n»e podkreślaliśmy, jednak zakładaliśmy, że obraz punktu jest też punktem. Inaczej mówiąc, twierd/ih-

523