3tom207

416

6. GOSPODARKA ELEKTROENERGETYCZNA

albo po przekształceniu

K_n, = MiAP_s+k_rAgJ4-k^E,+k_rAE_br)    (6.68)

gdzie: k_P — jednostkowy roczny koszt strat mocy czynnej, zł/(kW • a); AP, — straty mocy czynnej przy obciążeniu szczytowym linii lub stacji, kW; k_Q —jednostkowy roczny koszt strat mocy biernej, zł/(kvara); Ag, — straty mocy biernej przy obciążeniu szczytowym linii lub stacji, kvar; k_E — jednostkowy koszt strat energii czynnej, zł/(kW-h); AE_r — roczne straty energii czynnej, kW h./a; k_FJt — jednostkowy koszt strat energii biernej, zł/(kvarh); A— roczne straty energii biernej, kvar-h/a; k_e — ekonomiczny równoważnik mocy biernej; 5, — współczynnik udziału w szczycie systemu, wyrażony jako

K

P,

(6.69)

gdzie: F_s — obciążenie rozpatrywanej linii lub stacji występujące w czasie szczytowego obciążenia systemu, P, — obciążenie szczytowe tej linii lub stacji, które może występować w innym czasie niż obciążenie szczytowe systemu.

Wobec tego całkowite koszty roczne wytwarzania energii w elektrowni lub przesyłania energii za pomocą linii i stacji, wyrażone w zł/a, oblicza się ze wzoru

(6.70)

(6.71)

K_r = K_n + K_e = K_n+K„+K_a = K,+K. przy czym roczne koszty stałe

K, = K_n+K_cs

oraz roczne koszty zmienne

K. = K„    (6.72)

Po podzieleniu całkowitych kosztów rocznych K, przez energię roczną £, otrzymuje się jednostkowy roczny koszt energii, wyrażony w zł/(kW • h)

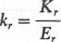
Jako kryterium optymalności przy porównywaniu różnych rozwiązań technicznych w zakresie inwestycji w elektroenergetyce oraz eksploatacji urządzeń i obiektów elektroenergetycznych przyjmuje się minimalizację całkowitych kosztów rocznych

K_r -* min    (6.74)

a w niektórych przypadkach, które omówiono w p. 6.3.3, dopuszcza się również jako kryterium przybliżone — minimalizację jednostkowych kosztów rocznych

K_r

k_r =--» min    (6.75)

6.3.2. Rozkłady czasowe nakładów i efektów

Rozkładem czasowym prostym nazywa się taki rozkład nakładów niezbędnych do uzyskania zamierzonego efektu, w którym cały nakład inwestycyjny K„ jest skupiony w ciągu jednego roku zwanego umownie rokiem zerowym (zwykle jest to rok poprzedzający rozpoczęcie eksploatacji), zaś koszty eksploatacyjne K_e oraz uzyskane efekty produkcyjne E są jednakowe we wszystkich następnych latach i = 1,2

6J. OBLICZENIA GOSPODARCZE W ELEKTROENERGETYCE

417

Rozkład czasowy złożony polega na tym, że nakłady inwestycyjne K_n(__JI są rozłożone w kolejnych latach okresu trwania inwestycji od roku — M do roku zerowego włącznie (j = 0,l,~»AO, a koszty eksploatacyjne K„ i efekty produkcyjne £, są zróżnicowane w kolejnych latach okresu eksploatacji (i = 1,2,..., N).

W tablicy 6.6 przedstawiono schematycznie powyższe rozkłady czasowe nakładów i efektów dla całego okresu trwania obiektu od pierwszego roku okresu inwestycji —M do ostatniego roku okresu eksploatacji N.

Tablica 6.6. Rozkłady czasowe nakładów i efektów

Okresy	Okres inwestycji	Okres eksploatacji
Rok	—M ... -j ... -2 -1 0	1 2 ... i ... N-i N
Rozkład czasowy prosty
Nakład inwestycyjny Koszt eksploatacyjny Efekt produkcyjny	- ... - ... - - K.	K, Kr ... K, ... K, Kr E E ... E ... E £
Rozkład czasowy złożony
Nakład inwestycyjny Koszt eksploatacyjny Efekt produkcyjny	U) *** ^«<-/) — ^*-1) K*o	... K„ ... - /C„ Ke2 ... ... K,, Ej E2 ••• £,• ••• &N- 1
Zastępczy rozkład czasowy prosty, równoważny rozkładowi złożonemu
Nakład inwestycyjny Koszt eksploatacyjny Efekt produkcyjny	- ... - ... - - fC„	K„ ... K„ ... K„ K„ Er Er ... E, ... Er E,

W przypadku rozkładu czasowego prostego całkowite koszty roczne K_r i jednostkowe koszty roczne k_r oblicza się ze wzorów (6.70) i (6.73). W przypadku rozkładu czasowego złożonego należy natomiast określić zastępczy rozkład czasowy prosty, stosując odpowiednie reguły rachunku dyskonta. Tak więc zdyskontowaną sumę nakładów inwestycyjnych K^, sprowadzonych do roku zerowego, określa się metodą dyskonta, czyli oprocentowania na procent składany, za pomocą sumowania

K_rJ =    +d)' + K^₂₎(l+d)²+... + K_ni__M)(] +d)^M    (6.76)

co można zapisać w skrócie jako sumę

I K«-flU+dy    (6.77)

i—o

Na rysunku 6.12 przedstawiono w sposób poglądowy mechanizm tworzenia zdyskontowanej sumy nakładów inwestycyjnych K_rJ. Jak widać z tego rysunku oraz ze wzoru (6.76), nakłady ponoszone w okresie trwania inwestycji są „zamrożone”, czyli nieczynne w produkcji, ponieważ nie biorą udziału w tworzeniu akumulacji, która rozpoczyna się

27 Poradnik inżyniera elektryka tom 3