bullock (14)

14

Rozdział 2 III C

miliwoltomierz

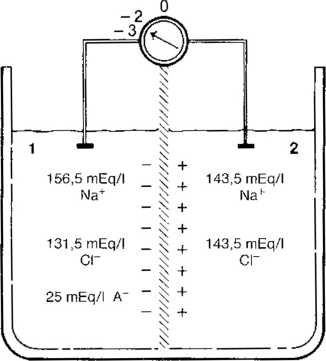
RYC. 2-1. Równowaga Donnana. Komora 1 jest naładowana ujemnie w porównaniu z komorą 2, stężenie substancji rozpuszczonych jest tu większe, większe jest także stężenie kationów (Na⁺) oraz mniejsze stężenie anionów dyfundujących (Cl^-). Ze względu na to, że aniony nie dyfundujące (A') znajdują się w komorze 1, potencjał błonowy po lewej stronie błony jest ujemny i można go wyliczyć z równania Nernsta dla jonu dyfundujące go. Roztwory nie znajdują się w stanie równowagi osmotycz-nej, ponieważ w komorze 1 jest więcej cząsteczek (obecność anionów niedyfundujących).

Wartość potencjału spoczynkowego określają: gradient stężeń oraz zdolność przenikania jonów przez błonę (przepuszczalność błony).

Obliczenie potencjału spoczynkowego błony. Wielkość spoczynkowego potencjału błonowego można obliczyć używając równania przenikalności (przewodnictwa błonowego) Goldmana.

1. Równanie przenikalności

Em ~ T_K • E_k + T_Na ■ E_Na + Tj_on • Ej_on +

...+ E

pompy ■

a. Wyjaśnienie skrótów

(1)    Ej_on - potencjał równowagi Nernsta, odpowiada energii zawartej w gradiencie stężeń każdego z jonów mającego zdolność przenikania przez błonę.

(2)    T_jon - przenikalność odpowiada względnej przewodności błony (g) dla każdego z jonów. Na przykład

Tk -

Rk

SK ⁺ gNa

oraz

gNa

&K ⁺ §Na

(3) E_pompy - potencjał błonowy wytwarzany przez pompę sodowo-potasową. Pompa Na-K wyrzuca na zewnątrz komórki 3 jony sodowe, a na ich miejsce wprowadza 2 jony potasowe, dlatego wnętrze komórki ma ładunek ujemny. Jednakże w większości komórek, oprócz komórek mięśnia sercowego, wartość potencjału pompy jest tak niewielka, że można ją zignorować, b. Przykład. W stanie równowagi wartość gj< jest około dziewięć razy większa od wartości g_Na. Dlatego:

^{Tk =} 9T1 ⁼ 0,9 oraz TNa = 9T1 ⁼ 0>1>

E_M = 0,9 • -92 mV + 0,1 • +60 mV = 76,8 mV.