Capture247

nic zmieniają się z próby nu próbę w żaden znany. *ystcn tvku matematycznym wartość prawdziwą można zdefinio™

rowc

W n./yku matcmaty/n\

wać

T_x = lim

n— N

gdzie X, odnosi się do Mego pomiaru. Zatem wartość prawd/m

której zbli/a się średnia arytmetyczna, w miarę jak liczba powtarza N wzrasta nieskończenie. Takie pojęcie wartości nrawd/iw.-.

i prawdziwej jc>t

pomiarów wielkości fizycznych. Możemy na przykład mierzyć dlu ,    ^^:

pomocą miary metrowej. Procedurę pomiarową możemy powtarza/J

zmienność wśród otrzymywanych pomiarów przypisywać błędów" \j....

jąć. że pomiar długości biurka da się powtórzyć znaczną liczbę razy w j,,.. stałych warunkach, w których ani biurko, ani miara metrowa mc /m en * żaden systematyczny sposób. Zwiększając liczbę pomiarów i obliczają _:>h ../ możemy ograniczyć błąd oszacowania wartości prawdziwej Teoretyczne możemy zmniejszyć tak bardzo, jak tylko chcemy, zwiększając liw'/bc Gdy liczba pomiarów staje się nieskończenie wielka, średnia /bli/a v_ę j I prawdziwej jako do granicy.

Można zadać pytanie, czy takie pojęcie wartości prawdziwej jo:    .,

do pomiarów wielkości psychologicznych. Oczywiście przy micr/cnm /. ludzkiego nic możemy zwykle powtarzać pomiarów znaczną liczbę y,... cecha może zmieniać się nieznacznie lub nawet poważnie w c/asic. :r ,. modyfikować sam proces wielokrotnego mierzenia. Na przykład mc uleęj wości. że przy dokonywaniu pomiaru inteligencji dziecka mc mo/erm pr.\; ... dzić tego samego testu inteligencji !(X) razy. aby otrzymać os/acowxnc Niezależnie ihJ wkładu pracy w tego rodzaju oszacowanie, wyniki. k>rc . libyśmy. byłyby bezwartościowe ze względu na wpływ wyćwiczenia. /    . .

innych czynników.

W tej sytuacji w psychologu stworzono wiele rozmaitych procedur błędu mc polegających na dokonywaniu serii pomiarów powtarzanych M -praktyczności szacowania błędu pomiarów psychologicznych /a pomocą ij: czby pomiarów powtarzanych, pojęcie wyniku prawdziwego jako średn:. skończenie wielu takich pomiarów pozostaje wciąż ważnym pojęciem w dno. badania błędów pomiaru. Możemy powiedzieć, że znaczenie pomiaru prawd; -..I jest tu analogiczne do znaczenia, jakie dla statystyki / próby ina parametr pp- I Różnica między statystyką z próby a parametrem populacji jest błędem Zwiększając wielkość próby, zmniejszamy zarazem wielkość błędu prób) ^ • padku populacji nieskończonej me obciążona statystyka z próby /bli/a mc - • rametru populacji jako do granicy, w miarę jak wielkość próby zbliża m, skonczonosci. Błąd próby jest błędem związanym /.e statystyką oparu ra :<*^T próbie pomiarów. Przez błąd pomiaru rozumie się zazwyczaj błąd zwią/J-nj /> • kretnym pomiarem stanowiącym oszacowanie wartości prawdziwej ^    ‘

4V0

24,2. Wpł> w błędu pomiaru na średnią i wariancję

Rozważmy populację pomiarów. Każdy pomiar obci$tooy jc-.i błędem i taoJte 10-,UĆ zapisany jako X, - T_t ♦ e„ gdzie .Y, jest pomiarem zaobserwowanym, a 7 pomiarem prawdziwym Dokonując sumowania po ws/ysdoch elementach populacji, otrzymujemy IX, = IT. «■ I*. JcżeR założymy. /_c M*! pomiaru jest błędem przypadkowym, jednakowo często mającym wannie dulainia i ujemn* możemy „pisać równanie Łf, = 0. W rezultacie suma pomiarów obciążonych błędem równa jot sumie pomiarów prawdziwych Wynika stąd równie/, ze sredn* z wartości prawdziwych i zaobserwowanych sa sobie równe, j zarazem równe średniej w populacji p. Możemy stad wyciągnąć wniosek, ze Nad pomiaru mc »>u«ra systematycznego wpływu na średnia arytmetyczna Średnia oparta na próbie V pomiarów nie jest w systematyczny sposób większa oru mnicj-za niż średnia z f*> miarów prawdziwych. Średnic oczekiwane z pomiarów zaobserwowanych i prawdziwych sa równe średniej w populacji p. czyli:

(242)

£<X) = £(T> = p.

Blad pomiaru wywiera wpływ na wariancje z próby średniej arytmetycznej. Zagadnienie to omówione zostało w podrozdziale 24.6

Błąd pomiaru wywiera systematyczny wpływ na wariancje Możemy zapisać równanie (X, - p) = (T, - p) + e,. Jeśli wielkość wyrażona tym równaniem p«ł-niesiemy do kwadratu, dodamy po wszystkich elementach populacji i podzielimy przez N_r czyli liczbę elementów w populacji, otrzymamy:

Kx, - n»^: ₃ Kr, - m!^: _{+    +} ?

N_r " N, N, ^sp

■ 1^1    • m) t gIII U • r ^Ł    ■ • mammm —    '    |    « I

prawdziwymi, trzeci człon tego równania przyjmuje wartość 0. wobec czego

Przy założeniu, że błędy pomiaiu sa przypadkowe » me skorelowane z wynikam.

*    _______ A uidtft* rttfO Uur żerny zapisać:

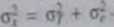
padków zarówno parametry populacji. _)A , _Wjrtołe, _prn,_d/mf

t24.3)

4**i