CCF20090120073

ści kinowej. Jak można by tego dokonać? Chcemy przedstawić fakt, że stan posiadania jakiegoś człowieka zaczął powiększać się — niech to będzie pierwszy sukces wynalazcy. Moglibyśmy pokazać, jak ów człowiek chowa pieniądze w kasie ogniotrwałej. W pierwszym tygodniu wkłada on do kasy jednego funta. W następnym tygodniu dodaje 2 funty. Następnie dodaje 3 funty. Jego zarobki z każdego tygodnia ułożone ,są w rulon zawierający o jednego funta więcej niż rulon z poprzedniego tygodnia.

Tak więc w x-tym tygodniu wynalazca odkłada x funtów szterlingów, a stale rosnący rulon monet uwidacznia ten fakt.

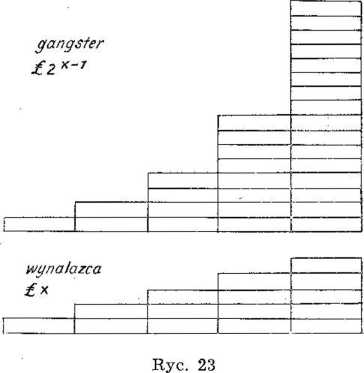
Ale akcja nie musi się na tym kończyć. Wynalazca ma przyjaciela-gangstera, który żyje z oszustwa i przemocy. Gangster chce dowieść, że nie warto być uczciwym. Namawia wynalazcę do zajęcia się tym, co daje dużo pieniędzy. Każdego tygodnia z pogardą umieszcza stos monet obok rulonu wynalazcy. W pierwszym tygodniu kładzie jednego funta; w drugim — 2 funty; w trzecim — 4 funty; w czwartym — 8 funtów, podwajając sumę w każdym tygodniu. Stały wzrost zarobków wynalazcy traci znaczenie. Może on odłożyć każdego tygodnia x funtów, a gangster 2^X_1 funtów (ryc. 23).

Te liczby nie tylko pokazują, że dochody wynalazcy i gangstera rosną. Uwypuklają one ponadto znaczenie różnych sposobów, w jakie te 'dochody rosną. Na tym polega zasadniczy sens wykresu, czyli rysunku, który unaocznia znaczenie jakiegoś wyrażenia matematycznego, jak x czy 2^x~^l.

W powyższym przykładzie rozpatrywaliśmy coś, co rośnie stopniami, nagłymi skokarM. Na przykład, tygodniowy dochód gangstera wzrósł z 4 funtów do 8 funtów, nie przechodząc poprzez -pośrednie wartości 5, 6 i 7 funtów. Możliwe jest jednak także, że pewna wielkość rośnie ciągle, tak jak roślina, bez skoków. Możemy — i zazwyczaj to robimy — sporządzić wykres ilustrujący ten ciągły wzrost. Jeżeli np. roślina rośnie w sposób ciągły zgodnie ze wzorem y —

— x (gdzie y oznacza wzrost rośliny w cm po x tygodniach), oznacza to nie tylko, że roślina mierzy 1 cm po 1 tygodniu i 2 cm po 2 tygodniach. Oznacza to również, że mierzy ona 1 —cm

1 1 1 ⁴

po 1tygodnia, 1—cm po 1— tygodnia itd.

Widzimy to na wykresie, w którym skoki zostały wygładzone (ryc. 24),

O tym, czy rysujemy krzywą ciągłą, czy krzywą rosnącą skokami, decyduje istota procesu, który wykres ma ilustrować. Wysokość rośliny, droga przebyta przez pociąg, ciężar dziecka dają wykresy ciągłe. Liczba dzieci w rodzinie, liczba miejsc w parlamencie posiadanych przez daną partię, liczba okrętów wojennych zmieniają się skokami.

149