CCF20090120123

na dwie sprawy: 1. metodę tę można zastosować do zagadnienia przebicia tunelu (ryc. 42); 2. metoda ta rzuca pewne światło na wspomniane wyżej znakii minus. Jeżeli podróżnik, po przebyciu opisanej wyżej drogi, przejdzie dalszych 30 km w kierunku 135° (tzn. na północny zachód), to jego przesunięcie się na północ wzrok-

N

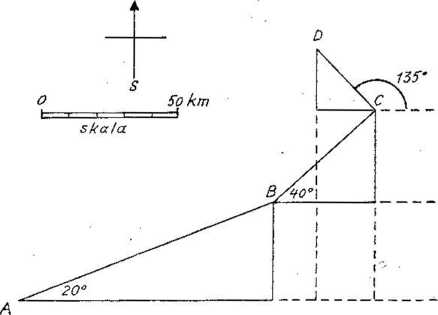
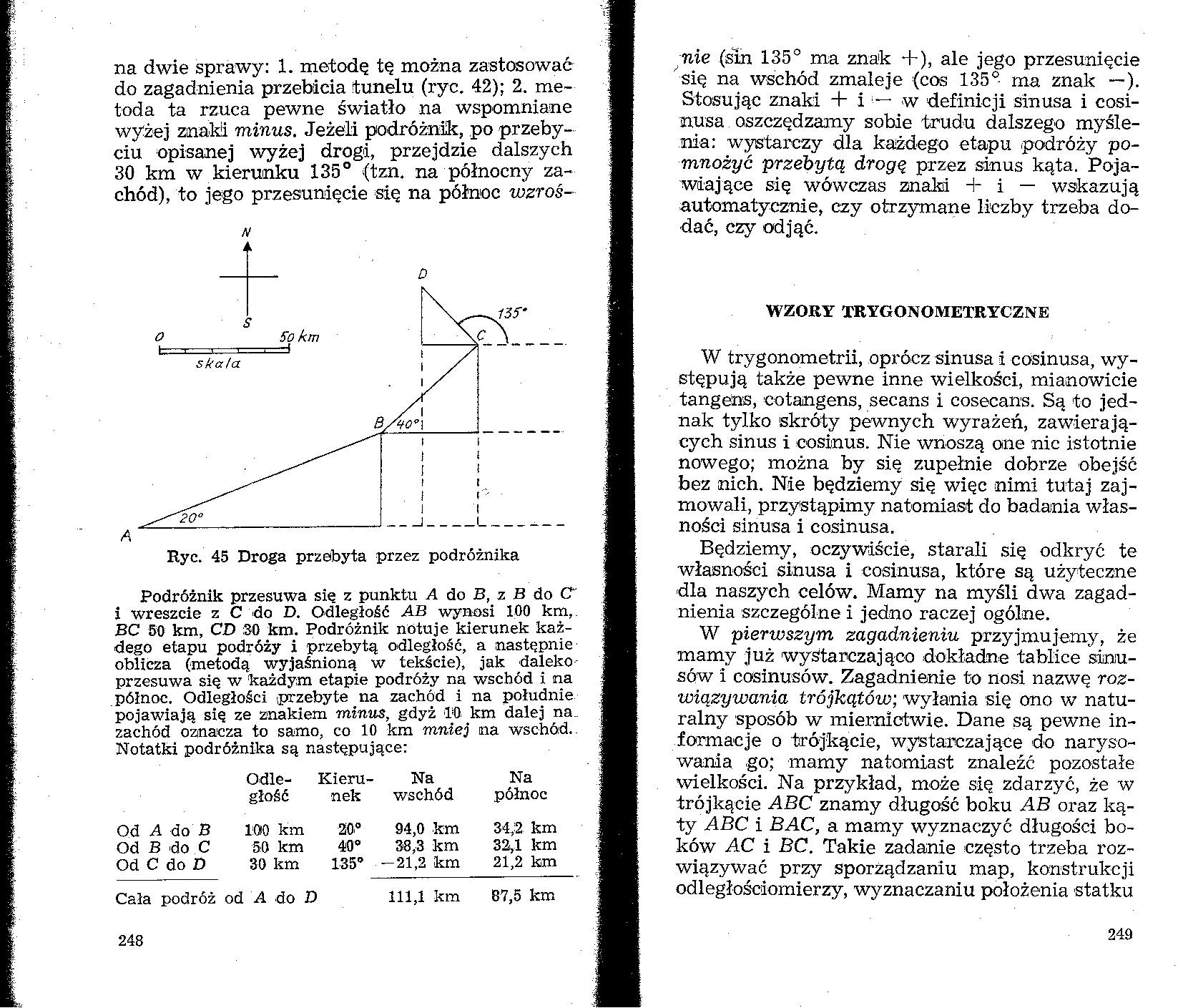
Ryc. 45 Droga przebyta przez podróżnika

Podróżnik przesuwa się z punktu A do B, zBdoC" i wreszcie z C do D. Odległość AB wynosi 100 km,. BC 50 km, CD 30 km. Podróżnik notuje kierunek każdego etapu podróży i przebytą odległość, a następnie oblicza (metodą wyjaśnioną w tekście), jak daleko przesuwa się w każdym etapie podróży na wschód i na północ. Odległości .przebyte na zachód i na południe pojawiają się ze znakiem minus, gdyż 10 km dalej na., zachód oznacza to samo, co 10 kra mniej na wschód.. Notatki podróżnika są następujące:

	Odle-	Kieru-	Na	Na
	glość	nek	wschód	północ
Od A do B	100 km	20'°	94,0 km	34,2 km
Od B do C	50 km	40°	38,3 km	32,1 km
Od C do D	30 km	135°	-21,2 km	21,2 km
Cała podróż od	A do D		111,1 km	87,5 km

nie (sin 135° ma znak + ), ale jego przesunięcie się na wschód zmaleje (cos 135°- ma znak —). Stosując znaki + i —- w 'definicji sinusa i cosi-musa oszczędzamy sobie trudu dalszego myślenia: wystarczy dla każdego etapu podróży pomnożyć przebytą drogę przez sinus kąta. Pojawiające się wówczas znaki + i — wskazują automatycznie, czy otrzymane liczby trzeba dodać, czy odjąć.

WZORY TRYGONOMETRYCZNE

W trygonometrii, oprócz sinusa i cosinusa, występują także pewne inne wielkości, mianowicie tangens, cotangens, secans i cosecans. Są to jednak tylko skróty pewnych wyrażeń, zawierających sinus i eosinus. Nie wnoszą one nic istotnie nowego; można by się zupełnie dobrze obejść bez nich. Nie będziemy się więc nimi tutaj zajmowali, przystąpimy natomiast do badania własności sinusa i cosinusa.

Będziemy, oczywiście, starali się odkryć te własności sinusa i cosinusa, które są użyteczne dla naszych celów. Mamy na myśli dwa zagadnienia szczególne i jedno raczej ogólne.

W pierwszym zagadnieniu przyjmujemy, że mamy już wystarczająco dokładne tablice sinusów i cosinusów. Zagadnienie to nosi nazwę rozwiązywania trójkątów; wyłania się ono w naturalny sposób w miernictwie. Dane są pewne informacje o trójkącie, wystarczające do narysowania go; mamy natomiast znaleźć pozostałe wielkości. Na przykład, może się zdarzyć, że w trójkącie ABC znamy długość boku AB oraz kąty ABC i BAC, a mamy wyznaczyć długości boków AC i BC. Takie zadanie często trzeba rozwiązywać przy sporządzaniu map, konstrukcji odległościomierzy, wyznaczaniu położenia statku

249