CCF20090120137

Możemy, rzecz jasna, kontynuować te działania i znaleźć wszystkie potrzebne nam wartości: /, g, h... W wyniku takiego postępowania otrzymujemy (co Czytelnik może sam sprawdzić):

« = 1, b = 0, c = -y, f. = 0, g = k = 0,

a więc

cos o:

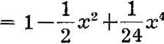
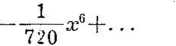
Reguła, według której otrzymujemy liczby 1, 2, 24, 720 itd., jest następująca. Zaczynamy od liczby 1. Mnożymy ją przez 1 razy 2; to daje nam drugą liczbę, 2. Drugą iliczbę mnożymy przez 3 razy 4 i otrzymujemy trzecią liczbę; mnożąc ją przez 5 razy 6 otrzymujemy czwartą liczbę itd. Różniczkując podany wyżej szereg znajdujemy szereg dla sin x:

120

sm x = x-

Szeregi te nadają się do celów rachunkowych, gdyż wyrazy ich maleją bardzo szybko i kilka pierwszych wyrazów szeregu daje dość dobrą odpowiedź. Szeregi te dają więc odpowiedź na postawione w rozdz. 13 pytanie, w którym chodziło o znalezienie sposobu utworzenia tablicy .sinusów i cosinusów bez sporządzania rysunków.

NIEBEZPIECZEŃSTWO STOSOWANIA SZEREGÓW

Szeregi miały duże znaczenie we wczesnym okresie istnienia rachunku różniczkowego i całkowego, szczególnie po 1660 r. Był to okres wielkiej aktywności praktycznej; ludzie interesowali się rozwojem nauki i zajmowali się rozmaitymi zagadnieniami praktycznymi — konstrukcją zegarów i teleskopów, sporządzaniem map i budową okrętów. Jeżeli jakaś metoda matematyczna dawała poprawne rozwiązanie jakiegoś zagadnienia praktycznego, ludzie nie zastanawiali się, czy jest ona logiczna, czy nie. Operując małymi ■przyrostami, Aa:, matematycy postępowali, jak im było wygodniej: czasem mówili, że Aa: jest bardzo małe i wygodniej będzie traktować Aa: jako równe zeru. Nieco później chcieli wykonać dzielenie przez Aa:, mówili .więc: „Jeżeli Ax jest równe zeru, to nie można dzielić przez Ax; założymy więc, że Ax jest małe, ale nie jest równe zeru”. To, co im było w danej chwili wygodniejsze, przyjmowali za prawdę. Jeżeli odpowiedź okazywała się fałszywa, to całą swoją pracę wyrzucali do kosza. Ponieważ wyniki rozważań matematycznych porównywano zawsze z praktyką, więc ta niewyszukana metoda działała zupełnie dobrze.

■Podobnie postępowano z szeregami. Jeżeli wydawało się rozsądne uczynić pewien krok, to krok ten robiono. Jeżeli jednak krok ten dawał absurdalny wynik, uznawano, że coś jest nie w porządku.

Po blisko 150 latach beztroskiej matematyki pojawiły się pewne kłopoty. Przy Obliczaniu np.

log a rytmów pojawia się szereg 1—+ 4---7+

11    2    3    4

+-g---g-+... Połowa wyrazów tego szeregu ma

277