CCF20090120141

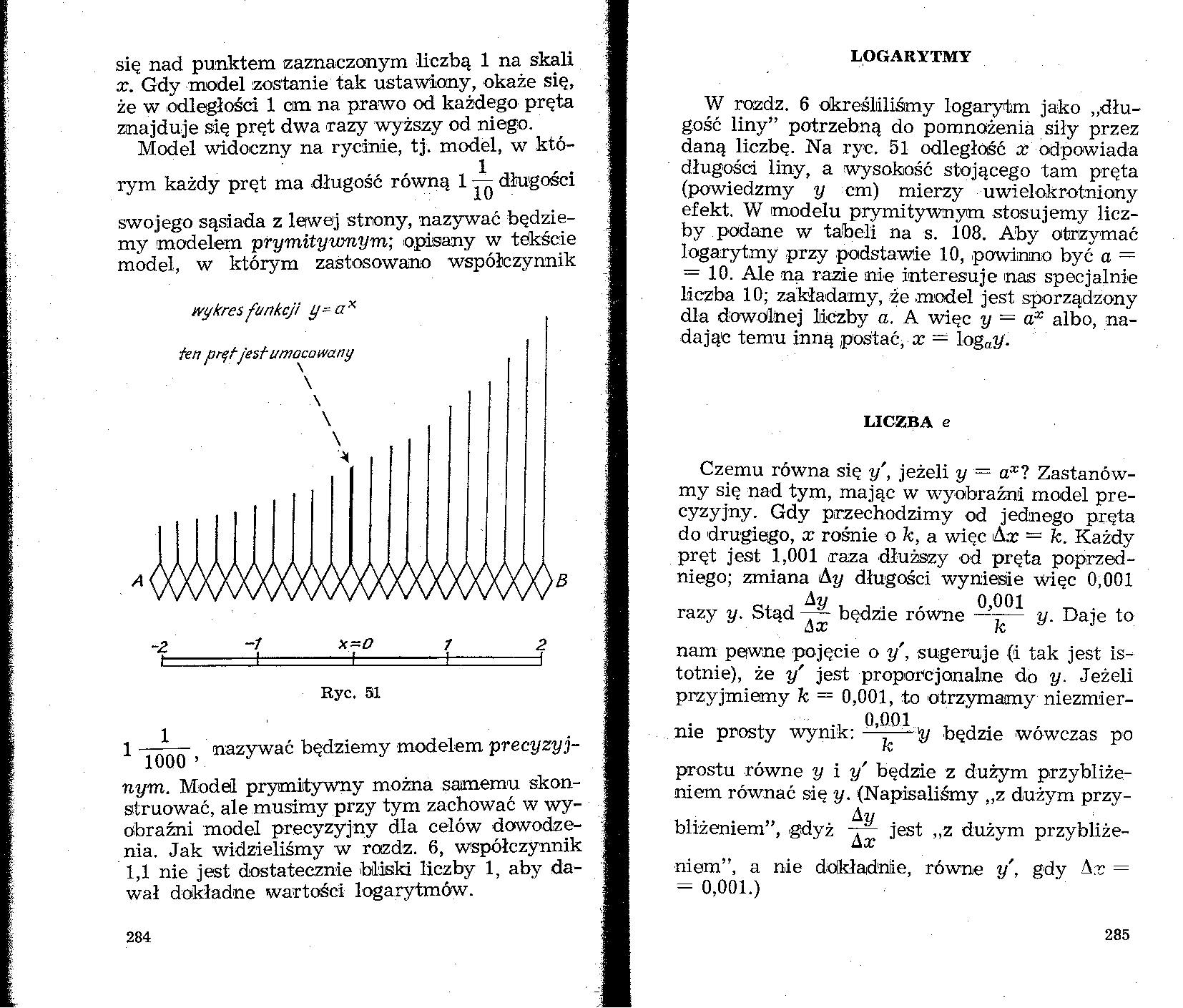
się nad punktem (zaznaczonym liczbą 1 na skali x. Gdy model zostanie tak ustawiony, okaże się, że w odległości 1 cm na prawo od każdego pręta znajduje się pręt dwa razy wyższy od niego.

Model widoczny na rycinie, tj. model, w którym każdy pręt ma długość równą 1 — długości

swojego sąsiada z lewej strony, nazywać będziemy modelem -prymitywnym; opisany w tekście model, w którym zastosowano współczynnik

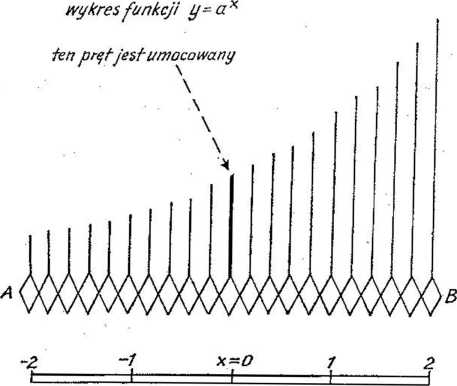
Ryc. 51

1 ■ j——_} nazywać będziemy modelem precyzyjnym. Model prymitywny można samemu skonstruować, ale musimy przy tym zachować w wyobraźni model precyzyjny dla celów dowodzenia. Jak widzieliśmy w rozdz. 6, współczynnik 1,1 nie jest dostatecznie bliski liczby 1, aby dawał dokładne wartości logarytmów.

W rozdz. 6 określiliśmy logarytm jako „długość liny’’ potrzebną do pomnożenia siły przez daną liczbę. Na ryc. 51 odległość x odpowiada długości liny, a wysokość stojącego tam pręta (powiedzmy y cm) mierzy uwielokrotniany efekt. W modelu prymitywnym stosujemy liczby podane w tabeli na s. 108. Aby otrzymać 1 ogarytmy przy podstawie 10, powinno być a = = 10. Ale ną razie nie interesuje nas specjalnie liczba 10; zakładamy, że .model jest sporządzony dla dowolnej liczby a. A więc y = a^x albo, nadając temu inną postać, x — log_ay.

LICZBA e

Czemu równa się y , jeżeli y ~ a^x? Zastanówmy się nad tym, mając w wyobraźni model precyzyjny. Gdy przechodzimy od jednego pręta do drugiego, x rośnie o k, a więc Ax = k. Każdy pręt jest 1,001 .raza dłuższy od pręta poprzedniego; zmiana Ay długości wyniesie więc 0,001

k

razy y. Stąd będzie równe —yy- U- Daje 1°

nam pewne pojęcie o y, sugeruje (i tak jest istotnie), że y' jest proporcjonalne do y. Jeżeli przyjmiemy k = 0,001, to otrzymamy niezmier-.. 0,0.01 , , .

me prosty wynik:    ■■ y będzie wówczas po

rC

prostu równe y i y będzie z dużym przybliżeniem równać się y. (Napisaliśmy „z dużym przy-Ay

bliżeniem”, .gdyż jest „z dużym przybliżeniem”, a nie dokładnie, równe y', gdy Ax = = 0,001.)

285