CCF20091206017

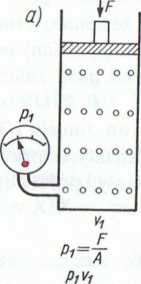
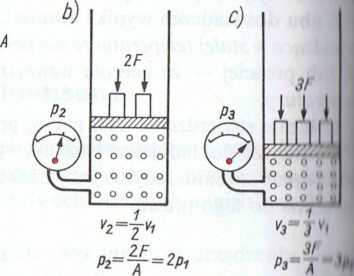
Temperatura T=const

Wz    PsV,

Rys. 3.2. Ilustracja prawa Boyle’a i Mariotte’a, czyli zaloż.liuf ciśnienia gazu od jego objętości w stałej temperaturze: ul i.ui

początkowy, b) i c) proporcjonalnie do wzrostu ciśnienia .....I< |»

objętość gazu

Ciśnienie p—const

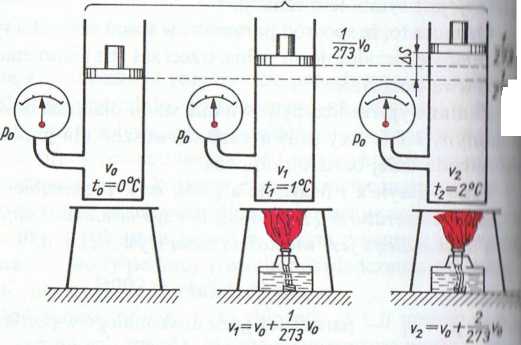
Rys. 3.3. Ilustracja prawa Gay-Lussaca. W miarę podgrzewania inin przy stałym ciśnieniu wzrasta jego objętość. Przesuwając ciężar (tli >11 m drodze ds, gaz wykonuje pracę

i ihi/m ciśnieniu stosunek wartości objętości właściwej gazu li ic n\'ch stanach jest równy stosunkowi jego temperatury, ftp/ ic skuli Kehiria

(3.3)

-L = 1l ^V2 T₂

hm l lnuIcsa głosi, że przy stałej objętości stosunek wartości T/M iic u w dwóch różnych stanach jest równy stosunkowi jego tylut i' o skali Kelvina

Pi_

Pi

II

t₂

(3.4)

Pt iw* Av«gatira

'<#......Ungiidra głosi, że różne gazy doskonałe znajdujące się w tej

'Ni

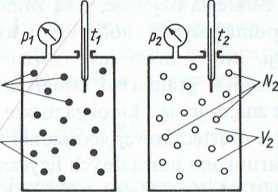
Pl~p2

ti=t_z

Vi=V₂

Rys. 3.4. Ilustracja prawa Avogadra

hMH|M'i ii turze i pod tym samym ciśnieniem w takiej samej H»i t >ii wiórują jednako->#la i /i|'ileczck.

Im uświadomić sobie Itniin |r wynikające Avogiulra (rys. 3.4),

||t |Mnl uwagę dwa róż-iM‘i iliwikoiiałe 1 i 2;

-i"/i»uy z /V, cząs-u Mianie cząsteczko-I, di ii(ii zań składający I A/, i /i|Nliii:zek o masie

%|»#|miwi'| M₂. Masy obu gazów można wyrazić wzorami

m₂ — N ₂M 2

(3.5)

m, = N_lM₁;

........ It z wykorzystać zależność masy gazu od jego objętości V

|d .i r Wówczas otrzymamy następujące zależności

(3-6)

m,

Keii m₂ = V₂Q

ImIi nim gazy znajdują się w jednakowych warunkach (p_x = p₂ |t, i i zajmują taką samą objętość V_x = V₂ = V, to — zgod-

Mit .• i.. linii /mi 49