DSC05315

314 • liytaimr zagadnienia geodezji w epoce GPS

ni

H₄ = 40136 +148.72(7*-237J6)m, H, • llOOOm,

natomiast h - oznacza wysokość horyzontalną satelity. W niektórych algorytmach redukcji wyników obserwacji satelitarnych stosuje się modyfikację tego modelu dokonaną przez Goada i Goodmana. Znane są też inne modele refrakcji troposferycznej, np. Saastamoinena, Błocka i innych. Przytaczamy poniżej wzór Saastamoinena stosowany powszechnie w Europie:

w którym 2 oznacza kąt odległości zenitalnej satelity.

Szczególne podejście do modelowania refrakcji troposferycznej na podstawie pomiarów parametrów atmosfery prowadzonych na stacjach pomiarowych na powierzchni Ziemi jest wymagane w terenie górzystym, gdy stacje te znacznie różnią się wysokościami. W takich przypadkach pożądany jest pewien różnicowy model refrakcji troposferycznej (zob. Gurtner i in, 1989).

Pozytywne rezultaty przyniosło stochastyczne podejście do refrakcji troposferycznej (Trolli i in., 1990). Wykorzystano fakt, że stosunkowo łatwo i dokładnie można modelować współczynniki tej refrakcji w ‘suchym powietrzu’. Odpowiedni model jest opisany za pomocą następujących ogólnych zależności:

Sr_ślw(h)*f^KK)6rZ (1+&J,

fj_lw(h, R) jest pewną funkcją wysokości satelity nad horyzontem h oraz wektora R parame-tryzującego tzw. 'neutralną atmosferę*. Indeksy (*,) odnoszą się odpowiednio do 'suchej' i ‘wilgotnej atmosfery*, zaś wskaźnik (*) oznacza poprawkę refrakcyjną w zenicie. Jak już zaznaczyliśmy, współczynniki modelu dla 'suchej atmosfery* mogą być wyznaczone na drodze deterministycznej. W takim przypadku tylko te odnoszące się do ‘wilgotnej atmosfery' są przedmiotem zainteresowania. Należy wyznaczyć pewien współczynnik skalowy £ modelu oraz poprawkę do refrakcji w zenicie v. W modelu mogą być także uwzględnione zmiany czasowe wynikające z opóźnień troposfoycznych. Włączając taki model poprawek troposferycz-nych w proces wyrównania obserwacji GPS wyznacza się jego parametry, a następnie odpowiednie poprawki ze względu na refrakcję troposferycznądla poszczególnych obserwacji - lub częściej - poprawki do pozycji stacji obserwacyjnych. Szacuje się, że w wyniku takiego podejścia błędy z tytułu refrakcji troposferycznej, związane ze składnikiem wynikającym z wpływu ‘wilgotnej atmosfery*, zostają zredukowane do wartości mieszczącej się w przedziale I + S cm, a przy większej liczbie satelitów (5 > 4), odpowiednio rozmieszczonych (na różnych wysokościach horyzontalnych), nawet do kilku milimetrów. Ogólnie, w wyniku podejścia stochastycznego, otrzymano wyniki bardzo zbliżone do tych, jakie udaje się osiągnąć stosując pomiary zawartości pary wodnej za pomocą radiometrów WYR (King I In, 1989).

Refrakcja Jonosferyczna

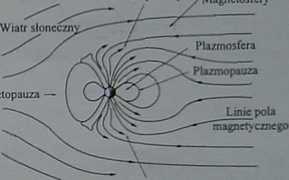
Wspominaliśmy już wyżej, że istota refrakcji jonosfeiycznej polega na opóźnieniu fil ciek-tromagnetycznych przez swobodne elektrony i jony, którymi zapełniona jest pewna część J przestrzeni wokółziemskiej. Aczkolwiek umownie przyjęto traktować jako jonosfere obszar wokół Ziemi od około 100 do około I 000 km, to w rzeczywistości struktura przestrzenna ziemskiej plazmosfery jest bardzo złoZona (zob. rys. 634). Wynika ona z kilku czynników, głównie: ze zmiennego w czasie promieniowania Słońca, z odziaływania promieniowania kosmicznego, ze struktury pola magnetycznego wirującej Ziemi, ze zmienności cienia Ziemi na skutek jej ruchu wirowego, a także z innych zjawisk sezonowych.

Odziaływanie jonosfery jest bardzo różnorodne. Nas interesują głównie dwa efekty: spowolnienie modulacji fali nośnej wysyłanej przez satelity GPS i przyśpieszenie fazy tej J fali. Pierwszy efekt, nazywany także opóźnianiem Jonosferycznym, sprawia pozorne wydłużenie drogi przebiegu sygnałów satelitarnych; przyśpieszenie fazy fali nośnej sprawia, że prędkość fazowa v_ę - A/moźc być większa od prędkości światła w próżni c i w efekcie ( oznacza pozorne skrócenie drogi stacja-satelita.

Wiatr polarny Magnetosfery

Magnctopauza

V

Wiatr polarny

Rys. 634. Ogólny pogląd na strukturę ziemskiej plazmosfery

Wzór opisujący refrakcję jonosferyczną ma swoje źródło w równaniu dyspersyjnym i współczynniku załamania (por. Feynman i in. 1969, s. 87). Fazowy współczynnik załamania można rozwinąć w następujący szereg potęgowy wyrazów odwrotnie proporcjonalnych do parzystych potęg częstotliwości:

/’ i

+..., (e,,e₄,... - współczynniki),

którego dwa pierwsze wyrazy można zapisać w postaci zależności