DSCN0498

I. Wprowadzenie

I. Wprowadzenie

r*ofw*nła lewa

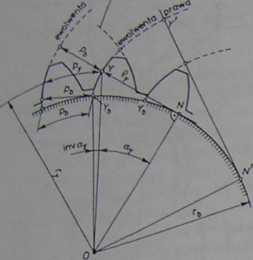
Z wzoru (1.21) wynika, że

Rys. 1.23. Parametry uzębienia ewolwentowego

(1.22)

2ir

p_b = ~r^rb = xr_b.

gdzie r jest podzialką kątową zębów:

2n

(1.23)

Wzór (1.22) można wykorzystać do obliczenia podziałki na dowolnym okręgu o promieniu r_T:

Py — ^xry    (1.24)

Odwijając myślowo napiętą nitkę z koła zasadniczego (jak do rysowania ewolwenty) widzimy, że podzialka zasadnicza po rozwinięciu z luku Y_b Y_b jest odległością p_b pomiędzy jednoimiennymi, prawymi lub lewymi, zarysami sąsiednich zębów. W tym przypadku jest ona mierzona po linii prostej, prostopadłej do zarysów ewoIwentowych, a zarazem zawsze stycznej do koła zasadniczego. Dla pary współpracujących kół prosta taka, przechodząca przez punkt styku zębów, jest linią przyporu i stąd p_b nazywane jest czasem podzialką przyporu. Jak to widać na rys. 1.21, współpracować ze sobą mogą koła o takiej samej wartości podziałki zasadniczej.

Rozpatrzmy tu jeszcze specyficzne zazębienie zębatkowe, w którym współpracują ze sobą koło zębate i zębatka. Zębatkę potraktujemy jak koło o nieskończenie dużej liczbie zębów. Zarysem zęba zębatki jest linia prosta jako szczególny przypadek ewolwenty odwijanej z okręgu zasadniczego o nieskończenie dużej średnicy. Dla zębatki (rys. 1.24) można określić odległość p pomiędzy sąsiednimi zębami jednoznacznie jako odległość między symetralnymi tych zębów lub jako

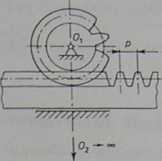
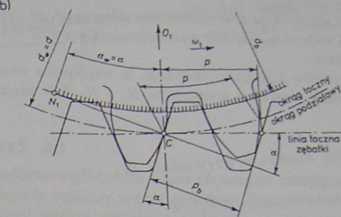
Rys. 1.24. Parametry zazębienia zębatkowego

odległość między jednoimiennymi zarysami bocznymi kolejnych zębów, mierzoną wzdłuż dowolnej linii równoległej do wierzchołków zębów. Odległość ta jest podzialką nominalną uzębienia i nazywamy ją krótko podzialką, oznaczając symbolem p dla odróżnienia od zdefiniowanej już wcześniej podziałki zasadniczej p_b. Podziałka zasadnicza występuje też w zębatce. Jest to odległość między jednoimiennymi zarysami bocznymi sąsiednich zębów, ale mierzona wzdłuż normalnej do tych zarysów. Zależność geometryczna między podzialką zasadniczą a nominalną jest widoczna na rys. 1.24 i można ją zapisać wzorem:

p_b — p cosa,    (1.25)

gdzie a jest kątem pochylenia bocznego zarysu zębów zębatki i jako nominalny kąt zarysu jest istotnym parametrem, warunkującym geometrię uzębienia ewołwen-towego.

Poprzednio stwierdziliśmy, że koła ewolwentowe mogą współpracować ze sobą wówczas, gdy mają jednakowe podziałki zasadnicze. Teraz, na podstawie wzoru (1.25), możemy sformułować warunek równoważny, a mianowicie: różne koła zębate ewolwentowe można kojarzyć w pary prawidłowo współpracujące wówczas, gdy mają takie same podziałki nominalne i takie same nominalne kąty zarysu. Z tego uwarunkowania wynika, że przy ustalonej podziałce nominalnej (lub zasadniczej) oraz ustalonym nominalnym kącie zarysu ewolweniowego, koła o różnych liczbach zębów można wykonywać metodą obwiedniową narzędziem o takim samym kształcie. Jest to dodatkowa, istotna zaleta zazębienia ewolwentowe-go, gdyż umożliwia daleko posuniętą unifikację i normalizację drogich narzędzi.

Odmierzane na linii tocznej zębatki (rys. 1.24) podziałki nominalne p wyznaczają na okręgu tocznym koła także takie same podziałki nominalne, ale już po luku. Ten szczególny okrąg koła, na którym podziałka zębów jest równa podziałce nominalnej, nazywamy okręgiem podziałowym, a odpowiadającą mu średnicę -średnicą podziałową, oznaczaną symbolem </. Obwód koła składa się z podziałek,

3 - Przekładnie zębate