3545337085

20 I. Dwuwymiarowe transformacje geometryczne

Z wzoru (1.54) wynika, że skalowaniejest operacjąmultiplikatywną. W celu dwu- lub kilkakrotnego przeskalowania punktu można zatem najpierw obliczyć iloczyn odpowiednich stałych skalowania (oddzielnie w kierunku osi x ij), po czym dokonać jednego skalowania ze stałymi równymi otrzymanym iloczynom.

1.5.2. Obrót wokół ustalonego punktu

Niech na płaszczyźnie xy znajduje się ustalony punkt R o współrzędnych (x_R, y_R). Obrót punktu P wokół punktu R o kąt <p prowadzi do punktu P', który można uzyskać za pomocą następujących, kolejno wykonywanych przekształceń (zob. rys. 14):

•    przesunięcia punktu P o wektor - x_Ri - y_R j, w wyniku czego otrzymujemy punkt P_{ (przy tym przesunięciu punkt R zostaje przekształcony na punkt będący początkiem układu współrzędnych),

•    obrotu punktu P, wokół początku układu współrzędnych o kąt <p - w ten sposób otrzymamy punkt P₂,

• przesunięcia punktu P₂ o wektor x_R i    j, co daje szukany punkt P'.

y

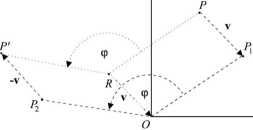
Rys. 14. Obrót punktu wokół ustalonego punktu

Jeśli użyjemy współrzędnych jednorodnych, to macierzą obrotu punktu P wokół punktu R o kąt <p będzie macierz, będąca iloczynem macierzy przekształceń składowych. Dla układu le-woskrętnego macierz ta będzie miała postać (zob. wzory (1.32) i (1.38))

(1.55)

	1	^0XR	costp	-sintp	0	1	0 -xR
Tj,T_y =	0	^1 yR	sintp	costp	0	0	^1 ~yR
	0	^0 1	0	0	1	0	^0 1

costp -sintp -a:^ costp + >>£ sintp +x_/f = sintp costp sintp costp +y_R ,

0

0

1