DSCN0563

162 5. Obliczenia wytrzymałościowe projektowe i sprawdzające

a następnie liczbę zębów zębnika:

Ostatecznie przyjmujemy znormalizowaną wartość modułu (tabl. 2.1). z_x musi być liczbą całkowitą, a więc najczęściej będzie zachodzić potrzeba skorygowania wyznaczonej wcześniej wartości średnicy zębnika.

Wartość naprężeń dopuszczalnych do wzoru (5.11) przyjmujemy

(5.13)

°Ff — 0,6a>|_iin i»

przy czym a_rhm, dobieramy z tabl. 5.14 lub z wykresów dla założonego materiału zębnika (rys. 5.16).

W obliczeniach wstępnych wymiarów uzębienia można posłużyć się też stosunkiem wielkości związanych b/m_n. Wprowadzając go do wzoru (5.11) oraz wstawiając d\ = ńi„otrzymujemy po przekształceniu:

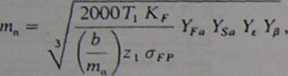
(5.14)

gdzie T, w niutonometrach, a a_FP w megapaskalach.

Stosunek h/m_n dobiera się w zależności od stanu ulepszenia zębów oraz od sposobu łożyskowania wałów, a więc podobnie jak stosunek b/d_x. Można przyjmować:

(5.15)

W specjalnych zastosowaniach wychodzi się poza podany tutaj zakres, .np. bfm„ < 6 dla wąskich kół w skrzyniach posuwów w obrabiarkach oraz b/m_n > 35 w ciężkich przekładniach turbinowych, przenoszących duże moce.

Wartość b/ii, dobieramy z tabl. 5.2, a z_x z tabl. 5.3, ale w niektórych przypadkach konieczne okaże się przyjmowanie wartości spoza podanych tam zakresów.

Wstępnego doboru liczby zębów zębnika można dokonać też za pomocą uproszczonego wzoru:

u+l

u

(5.16) V

$5

z tabl. 3.1 lub obliczanym Ży

; 1

gdzie W_z jest wskaźnikiem liczby zębów, dobieranym z tabl. 3.1 lub obliczanym z wzoru:

* <*hp Yjps sina cos a’

przy czym C_A * l-*-0,85 dla zębów prostych i C_A = 0,9-*-0,75 |

(5.17)

{

Tablica 53. Zalecane liczby zębów zębnika z₍

Materiał współ-	Przełożenie
pracujących kół	1	2	4	8
Stal ulepszana lub hartowana ze stalą ulepszaną HB < 230	32+60	29 +55	25+50	22+4S
Stal ulepszana lub hartowana ze stalą ulepszaną HB > 300	30+30	27+45	23+40	20+35
Żeliwo szare	26+45	23+40	21 +35	18 +30
Stal azotowana	24+40	21 +35	19 +31	16+26
Stal nawęglana	21 +32	19 +29	16+25	14+22

Dolne zakresy zaleca się stosować przy H| < 1000 obr/min, górne przy a, > 3000 obr/min.

Współczynnik obliczeniowy zęba na złamanie Y_p = Y_FS = Y_Fa Y_s, został opisany i objaśniony w pkt. 3.S. Jego wartość do wzorów (3.38), (5.10) i dalszych należy przyjmować z wykresów (rys. 5.18-5.20 oraz 5.28-5.30) w zależności od liczby zębów i współczynnika przesunięcia zarysu. Pewną trudność stanowi fakt, że w chwili korzystania z wzoru (5.17) nie znamy jeszcze ani liczby z_t, ani współczynnika przesunięcia zarysu x, . Dla ominięcia tej trudności założymy wstępnie, że zęby zębnika będą korygowane ze współczynnikiem Xi = 0,5 -r0,6. Jest to korzystny zakres korekcji, w praktyce często spotykany. Przy tym założeniu wartości Y_Pa i )$„ dobierane dla z, - 14 -ł-60 zmieniają się tylko nieznacznie i możemy w przybliżeniu przyjąć Y_FS = Y_Pa Y_Sa = 3,9.

Przyjmując dalej w uproszczeniu Y_c = 0,75 oraz dla zębów prostych Y_t = 1, możemy wzór (5.14) zapisać w postaci:

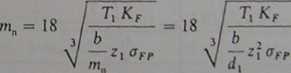
Widzimy, jak wiele uproszczeń i niepewnych założeń musieliśmy przyjmować w projektowaniu wstępnym, i rozumiemy, jak niezbędne będzie przeprowadzenie obliczeń sprawdzających i weryfikacji końcowej postaci konstrukcyjnej projektowanej przekładni zębatej.

Czasem dogodniejsze może się okazać dochodzenie do wstępnych wymiarów rfi, a i b na podstawie wskaźnika obciążenia Q_H, przyjmowanego z danych statystycznych w określonej branży maszynowej. Jeśli brak takich danych, to skorzystamy z wartości orientacyjnych zawartych w tabl. 3.1.