DSCN0597

230 5. Obliczenia wytrzymałościowe projektowe i sprawdzające

gdzie Kg., jest współczynnikiem uwzględniającym wpływ nierównomiernego obciążenia par zębów skośnych, przy dużym sumarycznym wskaźniku zazębienia; pozostałe symbole jak w pkt. 5.4.1,

Z badań doświadczalnych wynika, że przy dużych sumarycznych wskaźnikach zazębienia r... rośnie skłonność zębów do zatarcia, co uwzględniamy w obliczeniach za pomocą współczynnika K_By, przyjmując jego wartości z rys. 5.37 lub obliczając w przybliżeniu:

K,.f = 1	dla	e.. < 2, )
KB7- 1+0,2^	er-2H5-er) dla	2 <£., <3,5,>	(5.148)
KBi = 1,30	dla	ey£3,5. J

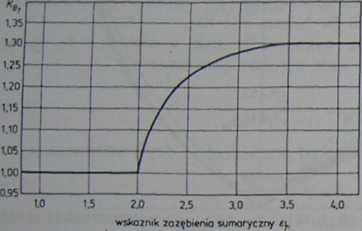
Rys. 5.37. Współczynnik skośności zębów K_Bt [N32]

Wartość lokalną umownego współczynnika tarcia, w dowolnym punkcie y na linii przyporu, można wyznaczyć z wykresu na rys. 5.38 lub obliczyć wzorem przybliżonym:

(5.149)

IV = 0.12

H

§, '°*²⁵

6nd,

Rys. S.38. Lokalny współczynnik tarcia zębów /i*, [N32]

gdzie w_n, — według wzoru (5.147), rj_M jest lepkością dynamiczną oleju w tempera* turze masy zębów, v_L — sumą prędkości stycznych w chwilowym punkcie przy-poru:

Ur = o_kl + v_k2 = ^2+r_y-^jtłsina_lw.    (5.150)

R_a jest parametrem chropowatości, średnią arytmetyczną chropowatości:

K_B-0,5(K_fll+K.₂),    (5.151)

R_af i R_a2 to średnie arytmetyczne chropowatości zębnika i koła (dla kół testowych 'często R_a = 0,35 pm), Q_lcd jest zastępczym promieniem krzywizny zębów w punkcie przyporu:

(l + r_y)(u-r_y) sin«„ ^fted (1+m)²    ° cos *

(5.152)

pozostałe parametry bez zmian.

Wprowadzając do wzoru (5.149) parametry dla bieguna zazębienia, otrzymujemy

/W = 0,12

( wflf	( R. Y'”
Wil^UEc)	Ve,cdc/

(5.153)

gdzie znaczenie symboli jest takie jak poprzednio, oraz:

Pjr = 2t>sinx_lw

BtalC

(1+u)² cos f}_b

(5.154)

(5.155)

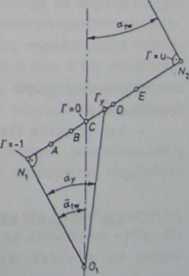
Występujący we wzorach (5.150) i (5.152) parametr linii zazębienia f jest bezwymiarową współrzędną liniową na linii zazębienia. Oo jego określenia posłu-

Rys. 5.39. Rysunek pomocniczy do określenia parametru r