DSCN0578

192 5. Obliczenia wytrzymałościowe projektowe i sprawdzające

zależności od potrzeby i charakteru obliczeń oraz od kompletności naszych informacji o parametrach potrzebnych do dokładnych wzorów.

K_hf — współczynnik rozkładu obciążenia uwzględnia zmianę obciążenia na jednostkę szerokości wieńca zębatego wskutek nierównomiernego przylegania pod obciążeniem. Uzasadnienie wprowadzenia tego współczynnika, oznaczonego ogólnie X,. zostało podane w pkt. 3.11, a tutaj przedstawimy metodykę i wzory operacyjne według normy [N3I] do obliczenia jego wartości. Współczynnik rozkładu obciążenia w zastosowaniu do naprężeń stykowych oznaczymy symbo-iem Kftf, a w zastosowaniu do obliczeń naprężeń gnących w podstawie zęba — symbolem K_r/. Współczynnik ten można określić w wyniku:

—    doświadczalnego wyznaczenia śladu przylegania zębów pod obciążeniem (potrzebny jest obiekt badań — przekładnia) lub

—    obliczenia efektywnego przekoszenia zębów.

Jeśli ślad przylegania zębów pod obciążeniem nie obejmuje całej szerokości b wieńca (rys. 3.16), lecz tylko część b_ol, to

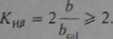
Sam ślad przylegania najłatwiej można wyznaczyć za pomocą tuszu lub specjalnych farb nakładanych na sprawdzane zęby, chociaż istnieją też jeszcze inne sposoby. Uzyskuje się tu w zasadzie sumaryczny efekt przekoszenia zębów jako wynik odchyłek wielu wymiarów przekładni oraz odkształceń pod obciążeniem. Stopniując wielkość obciążenia przy sprawdzaniu śladu przylegania zębów, można szacować wpływ poszczególnych czynników na przekoszenie sumaryczne. Taki sposób wyznaczania K# jest możliwy wówczas, gdy mamy wykonany obiekt — przekładnię. Badanie śladu przylegania zębów jest często wykorzystywane przy montażu przekładni średnich i dużych, produkowanych pojedynczo lub w małych seriach oraz przy remontach takich przekładni.

Wyznaczenie współczynnika na drodze obliczeń wymaga określenia efektywnej odchyłki od linii zębaf_ky w następstwie odchyłek wykonawczych i odkształceń pod obciążeniem. Wielkość odchyłek zmienia się w sposób losowy, podobnie też obciążenie i związane z nim odkształcenie. Można więc mówić tylko o wartościach przybliżonych i statystycznych, ujmując je jako prawdopodobieństwo wystąpienia określonej, efektywnej odchyłki linii zęba. Dokładne obliczenia byłyby bardzo pracochłonne i żmudne i wobec tego korzystamy często z metod przybliżonych, a jedną z nich jest metoda, którą tutaj przedstawimy, przyjęta w normie [N31].

Przy założeniu liniowego rozkładu obciążenia na rozpatrywanej długości zęba oraz dla zakresu 1 <    < 2,5 stosować można wzór:

gdzie współczynniki K_A i K„ określono już poprzednio, /.₀ jest odkształceniem zazębienia wolnego od odchyłek wykonawczych (bezbłędnego) według wzoru (5.71), f_ky — efektywną odchyłką linii styku zębów od położenia poprawnego (rys. 5.10), C = 0,4 — stalą dla zębów hartowanych powierzchniowo, a C = 0,3 — stałą dla zębów normalizowanych lub ulepszanych.

Wartości f.₀ obliczamy wzorem:

⁰ bc' cos a,

(5.71)

gdzie Z_t jest współczynnkiem uwzględniającym wskaźnik zazębienia (rys. 5.12), c - sztywnością właściwą pary współpracujących zębów według wzoru (5.67), a, — kątem przy por u czołowym, na okręgu podziałowym; pozostałe symbole jak poprzednio.

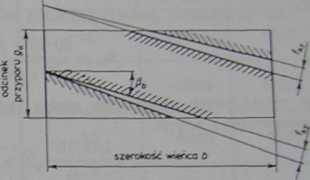
Rys. 5.10. Efektywne odchylenie położenia Unii styku zębów

Najbardziej uciążliwe jest określenie efektywnej odchyłki linii styku zębów f_kt, gdyż w grę wchodzi tu wiele parametrów, których wartość uzależniona jest od luzów w łożyskach, odchyłek wykonawczych, odkształceń sprężystych i dodatkowo uwarunkowanych zużyciem przy docieraniu. Stosujemy tu jeden z dwóch wzorów:

(5.72)

(5.73)

fky — \fkE+fkZr\~fkV<

fky = \fkt\ +fkZ ~fkVt

gdzie f_kE jest przekoszeniem zębów spowodowanym odkształceniami sprężystymi (głównie wałów) i luzem w łożyskach, f_kZ — przekoszeniem wynikającym z dopuszczalnych odchyłek wykonania, f#, — przekoszeniem rzeczywistym (pomierzonym) spowodowanym odchyłkami wykonawczymi, f_kV - przekoszeniem (złagodzeniem przekoszenia) w następstwie dotarcia.

Wzór (5.72) stosujemy wówczas, gdy dysponujemy wartościami pomierzonymi f_Ur, a wzór (5.73), gdy znamy tylko tolerancje wykonania.

13 — Pnckhómc zębufc