DSCN0598

232 3. Obliczenia wytrzymałościowe projektowe i sprawdzające

żymy się rys. 5J9, na którym przyjmujemy:

F = — 1 w punkcie Ni, r — 0 w punkcie C (biegun zazębienia), a przy założeniu liniowej zależności otrzymamy:

||gi dla punktu N₂.

W dowolnym punkcie oznaczonym indeksem y na linii zazębienia będzie zatem

J£5ł_i tg

■tyw

(5.156)

W pozostałych charakterystycznych punktach przyporu będzie: — w punkcie A

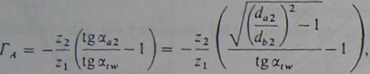
(5.157)

— w punkcie B

r_B = r_E-

2n

^zi tg w’

(5.158)

— w punkcie D

ro = rx+

2k

1 tg a. w’

(5.159)

— w punkcie E

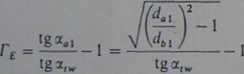
(5.160)

W ostatniej grupie wzorów przyjęto znaczenie symboli jak dotychczas oraz dodatkowo:

—    kąt przyporu (kąt zarysu) na walcu wierzchołkowym zębnika:

a_a, = arccos-p^-,    (5.161)

doi

—    kąt przyporu na walcu wierzchołkowym koła:

“.2

(5.162)

Wpływ cech materiałowych zębnika i koła, takich jak moduł sprężystości, przewodność cieplna i ciepło właściwe, na migawkowy przyrost temperatury uwzględniamy za pomocą współczynnika materiałowego X^. Będziemy go obliczać wzorem:

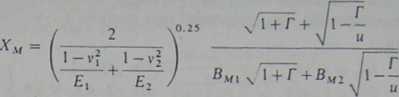
gdzie poszczególne symbole oznaczają: £, i £₂ — moduły sprężystości podłużnej (w N/mm²), v, i v₂ - liczby Poissona, a B_M, i Ś_M2 — cieplne współczynniki styku materiałów według wzoru (5.165) [w N/(mms^,,2K)].

Najczęściej zębnik i koło są wykonane ze stali, a więc £, = £,. v, = v₂ i B_Mi = fi_M2 i wówczas ostatni wzór uprości się do postaci:

i    ^ ⁼ (1-_V2)0 .25_Bm-    (5.164)

Cieplny współczynnik styku, zależny od przewodności i ciepła właściwego, wynosi

^ ^CV ■    (5.165)

W literaturze podaje się zwykle ciepło właściwe masowe i wówczas należy skorzystać z wzoru:

Cy = c_MQM,    (5.166)

j a przechodząc na jednostki przez nas użyte przybierze on postać:

c_v = 10~⁶c_mq_m.    (5.167)

We wzorach (5.165)—(5.167) poszczególne symbole oznaczają: X_M — przewodność cieplną [w N/(s • K)], c_v — ciepło właściwe na jednostkę objętości [w N/(mm²-K)], c_M — ciepło właściwe na jednostkę masy [w Nm/(kg-K)], a g_M -gęstość materiału (w kg/m³). Dla kół wykonanych ze stali ogólnie zalecanych do nawęglania i do ulepszania można przyjmować: |_M = 46 -=-50 N/(s-K), c_y v 3,8 N/(mm²-K), £ = 2,06-10⁵ N/mm², v = 0,3 i wówczas otrzymamy w uproszczeniu wartości przeciętne:

Bm = 13,6 N/(mm s^l/2 K),	(5.168)
XM = 50lCN^_3/4s^,'^2m~^l/2mm.	(5.169)

Współczynnik geometryczny X_B uwzględnia wpływ przełożenia i krzywizny zębów, od których z kolei zależy nacisk Hertza i poślizg zębów. Jest on funkcją