DSC07330

78

Macierze i wyznaczniki

	1	4 6 '		l-l 0 ' . i i		■ 1 1 0 ■
x =	O O	2 6 0 3 .		^0 2 2 o o i		0 11 .00 1

• Przykład 3.19

Jakie są możliwe wartości wyznacznika macierzy rzeczywistej A stopnia n, jeżeli:

a) A³ = A^T; b) A^T - A~^l = O; c) A³ + A~^x = O.

Rozwiązanie

W rozwiązaniu wykorzystamy następujące własności wyznaczników: det (A^T) = det A, det (A“^l) = (det A)~^l; det (A*) = (detA)^fc, gdzie fc€ N;

dci (o.4) = a° det A, gdzie n oznacza stopień macierzy A.

a)    Korzystając z tych własności kolejno otrzymamy

det [A⁷) = det (A^r) => (detA)³ = det A <=> det A = 1 lub det A = 0.

Zatem jedynymi możliwymi wartościami wyznacznika macierzy A są 0 i 1. Przyjmując .4 = f0| i .4 = |1| widzimy, że obie te wartości są realizowane.

b)    Korzystając z własności podanych na początku rozwiązania otrzymamy A^T -A~' = O <=> A^t = A~^l => det (A^T) = det (A^-1)

<=> det A — (detA)^-1 <=> det A = 1 lub detA = —1. Zatem jedynymi możliwymi wartościami wyznacznika macierzy A są liczby — 1 i 1. Przyjmując A = [1] i A = |—1| widzimy, że obie te wartości są realizowane.

c)    Korzystając, jak poprzednio, z przytoczonych na wstępie rozwiązania własności wyznaczników kolejno otrzymamy

A¹ + A~^l = O «=> A¹ = —A~' => det (A³) = det (-A^-1)

<=> (det A)³ = (-1)" (det A)^-1 <=> (det A)³ = (-1)“, gdzie n oznacza stopień macierzy A. Zatem jedyną możliwą wartością wyznacznika macierzy rzeczywistej stopnia nieparzystego jest liczba —1, a macierzy stopnia parzystego jest l. Przyjmując

A = [—11 oraz A =    j

widzimy, że obie wartości wyznacznika są realizowane.

Zadania

• Zadanie 3.1

a) Zaproponować opis, w formie macierzy złożonej z liczb całkowitych, położenia figur w grze w szachy. W jaki sposób można by sprawdzić, czy dana macierz odzwierciedla pozycję możliwą do uzyskania w czasie gry?

Zadania

79

b)    Zaproponować zapis, w postaci jednej macierzy, odległości drogowych i kolejowych w km między stolicami wszystkich województw w Polsce.

c)    Ekran monitora komputerowego jest złożony z 1024 x 768 punktów. Każdy punkt może świecić jednym z 20 kolorów. Kolorowe obrazy na ekranie można zapisywać w postaci macierzy złożonej z liczb całkowitych. Założyć, że ekran monitora przedstawia pierwszą ćwiartkę układu współrzędnych, z początkiem układu w lewym górnym rogu ekranu. Zapisać w formie macierzy przybliżony kształt ćwiartki kolorowej tęczy złożonej z pierścieni kołowych (rysunek).

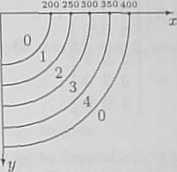
3) konstrukcja przestrzenna

Na rysunku:

0    - oznacza kolor biały,

1    - oznacza kolor niebieski,

2    - oznacza kolor zielony,

3    - oznacza kolor żółty,

4    - oznacza kolor czerwony.

d) Na rysunkach przedstawiono konstrukcje prętowe z ponumerowanymi węzłami:

1) plaski czworokąt z przekątnymi:    3) czworościan;

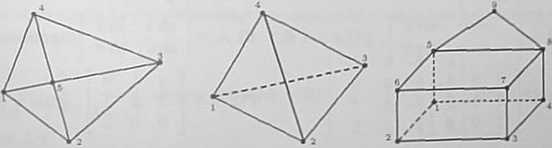
Zapisać w postaci macierzy schemat bezpośrednich połączeń między węzłami.

• Zadanie 3.2 Obliczyć:

a) 2

C)

1    5 3

2    -3 1

1	0
0	1
1	0
0	1
1	0

0 4 5 —la

2	-3	."5
■1	4	-2
3	-1	1

1    3 5

2    4 0'

	0 3'		‘0	0'
b)	1 1	+ 4	0	2
	! 0		1	1_

d)

cos a —sinal	[i COS0	- sin /31
sin a cos a J	[ sinjŚ	cos/9 J

f)[12345]-

5

4

3

2

1