DSC07319

60

Macierze i wyznaczniki

równy sumie ilocpuów odpowiadających sobie elementów i-tego wiersza macierzy A j¹ eSementuw kolumny macierzy B- Mamy

3 -4 5'		3 29'		'3■ 3 + (—4)-2 + 5-0 8• 29 + (—4)-18 + 5• (—3) .i
2 -3 1		2 16	= '	2-3 + (-3) ■ 2 + 1 • 0 2 - 29 + (—3)• 18 +1 - (—3) I
s_s -1		0-3		3- 3+ (-5) • 2 + (-1) -0 3• 29 + (-5) • 18 + (-1) • (-3)!

0 1 -1 0

d) Mamy

sin c coso		siup ca60
[-^10060 sino		—cos pl sin ,3

sin o sin 9 — cos a cos 3 sin a cos 0 + cos o sin 0 —cos.asin 0 — sinacos^ — cos acos.pl + sin a sin/3

—cos(o +0)    sin(a + 0)

-sin (a + 0) —cos(o + 0)

b) Rozwiązać układ równań macierzowych

X + Y 2X + 3 Y

1 1

0    l] ’

1    0

0 1 •

e) Mamy

	0"
1-1 1-^11	-1		10 + (-l)(-l) + l-2+(-lJ-(-3)‘		e”
-i l-» i|	2		(-1) - 0 +1 - (—1) + (—1)-2 + 1- (—3)		-8	■
	.-3.

RBMąaM

Dodawanie 1 odejmowani¹ m wierzy oraz mnożenie macierzy przez liczbę mają te son¹ *'■²,¹,.-. jak zwykle dzniams w zbiorze liczb rzeczywistych. W obu przykładach wyko-J rzyztemy te własności.

») Miony

-1 0

i 4

= X <=>

30 -3i 0

+ 3X +

-1 0 i 4

= X

«=¹ 3X - X =

1-Hia

<=>

Przykłady

~ — §g|

Rozwiązaniem równania jest macierz

b) Odejmując od drugiego równania podwojone pierwsze otrzymamy

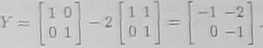
Odejmując teraz od drugiego równania potrojone pierwsze uzyskamy

fi Ol	Julii	-2 -3l
[01]	miii	L ^0"^2J

Zatem rozwiązaniem układu równań jest para macierzy

• Przykład 3.4

Obliczyć kilka początkowych potęg macierzy A, następnie wysunąć hipotezę o postaci macierzy Aⁿ. gdzie n G N i uzasadnić ją za pomocą indukcji matematycznej, jeżeli:

r r li		'10 r
a)-4= ‘	b) 4 =	010
[0-*J		101

Rozwiązanie a) Mamy

1

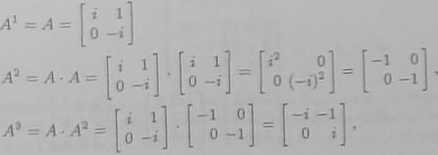
Przykład 3-3

2

a) Rozwiązać równanie macierzowe 3 ^ | ^ ^ j +    |^_^ 4 j = X;