Elektronikawzad67

W. Ciążyńnki PT.EX7K0NIKA W ZADANIACH

CTętó 2: Aiulua wpływu nriian tcmpctiluiy na pracę układów pólprccwudiukowych

W. Ciążyńnki PT.EX7K0NIKA W ZADANIACH

CTętó 2: Aiulua wpływu nriian tcmpctiluiy na pracę układów pólprccwudiukowych

zeru).

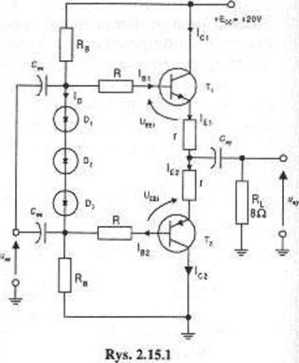
Zadanie 2.15

Dla pokazanego na rysunku 2.15.1 układu wzmacniacza mocy z parą komplementarną tranzystorów Tl (npn) i T2 (pnp) o idealnie symetrycznych charakterystykach mamy następujące dane w temperaturze odniesienia To = 25 °C:

-    prądy baz tranzystorów są równe i wynoszą po 1 mA;

-    prądy zerowe Icbo tranzystorów są równe i wynoszą po 2 pA;

-    współczynnik wzmocnienia prądowego dla każdego z tranzystorów wynosi P= 100;

-    spadek napięcia na przewodzącej diodzie i złączu baza-emiler wynosi 0,7 V niezależnie od płynącego prądu (tzn. rezystancje dynamiczne diod i złącz baza-emiter można przyjąć jako ró\

Przy wzroście temperatury o 40 °C można przyjąć:

-    przyrost wzmocnienia prądowego każdego z tranzystorów równy A(5 = 40;

-    przyrost prądu zerowego każdego z tranzy storów równy Alępo = 98 pA;

-    współczynnik temperaturowy zmian napięcia baza emiter i spadku napięcia na diodzie taki sam i równy c_BB = £o = - 2.5 mV / °C;

Należy obliczyć wartości rezystancji R_B, R i r zapewniających zakładane jednakowe i równe 1 mA prądy baz tranzystorów w temperaturze To, oraz kompensację zmian prądów kolektorowych w podanym zakresie temperatur.

Rozwiązanie

Jeśli prąd płynący przez R_B jest większy niż prąd bazy, o którym wiemy że wynosi 1 mA. oznacza to żc Id > 0, diody Dl - D3 przewodzą i możemy uważać, że spadek napięcia na nich wynosi 2,1 V. Wobec pełnej symetrii układu oznacza to, że na obydwa jednakowe rezystory Rn przypada napięcie 20 V - 2.1 V = 17.9 V. Na jeden z tych rezystorów przypada zatem 8,95 V, czyli zakładając płynący przez rezystor prąd około 2 mA dochodzimy do tego, żc można przyjąć rezystancję Rb równą np. 5 kD.

Wobec pełnej symetrii układu stały potencjał w punkcie do którego jest podłączony kondensator wyjściowy jest równy połowie napięcia zasilania, czyli ’ 10 V. Na napięcie 3 Uo = 2,\ V równe spadkowi napięcia na trzech diodach włączone są obwody baz obydwu tranzystorów. Dla tego zamkniętego obwodu mamy równanie „koła napięć”:

3t/₀ =2(C/_Si. + /_e R + l_rr)=2U_w + 2l„ R ₊ 2(fi + \)l, r a wobec równości Ube = Ud mamy: f/_n = 2/J« ₊ (/5 + l)r] skąd otrzymujemy:

/? + (/? + ₁)r = ^- = ^^ = 350n

21,    2 mA

Rys. 2.15.5

i ostatecznie dla /? = 100 warunek, który muszą spełniać rezystancje R i r. aby prądy baz obydwu tranzystorów były równe po 1 mA ma postać:

R +101 r = 350Q    (2.15.1)

Wtedy obydwa tranzystory są wstępnie spolaryzowane w taki sposób, że przy braku sygnału wejściowego płynie przez nie z zasilacza prąd Ic = fi' h= 100 • ImA = 100 mA. Prąd ten zwiększa moc strat we wzmacniaczu i obniża jego sprawność, ale jest to cena, którą płacimy za likwidację zniekształceń przebiegu wyjściowego, omówionych dla układu z zadania 1.13.

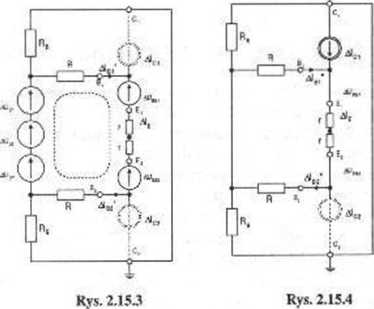
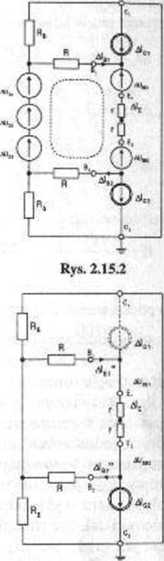
Do analizy zachowania się układu przy zmianach temperatury wykorzystamy schemat zastępczy przedstawiony na rysunku 2.15.2. Stosując zasadę superpozycji obliczamy trzy kolejne składowe przyrostów prądów baz dla obydwu tranzystorów (AI_B! i Alm).

Dla układu z rysunku 2.15.3 mamy składowe pochodzące od wszystkich SEM (przy wyłączonych SPM):

⁵¹ n 2{R + r)

Dla układu z rysunku 2.15.4 mamy składowe pochodzące od SPM równej Ala'

A/.. =-A1_c.-₇-r,

®^{l C,}2(/« + r)

R + 2r _A/-    R

(R+r)

‘^cl2(R₊r)

^A/"'^_A/<2 2(R+7)’

Dla układu z ry sunku 2.15.5 mamy składowe pochodzące od SPM równej Ala-R    .. R+2r

Na podstawie pełnej symetrii układu podstawowego i jego schematu zastępczego możemy napisać Alei = Alei— Ale- Całkowite przyrosty prądu bazy są wtedy także jednakowe i wynoszą:

, ₌iMJ -TM)„7r    ₍₂,₅₂₎

*    2(/? + r) 2{R + r)