Elektronikawzad59

W. OątyfStki F.I.FKTRON1KA W ZADANIACH

Częić 2: Analizo wpływu mian temperatury na pracę układów półprzewodnikowych

aby prąd Ic. mógł pozostać stały, przy wzroście temperatury należy doprowadzić do zmniejszenia prądu bazy /#. Musi się więc zmniejszyć rezystancja Rt. co spowoduje wzrost prądu h- Poniżej spróbujemy ocenić wartość liczbową współczynnika temperaturowego tej rezystancji.

Na podstawie powyższych zależności możemy napisać ogólne wyrażenie na interesujący nas prąd Ic w dowolnej temperaturze:

(2.10.2)

Aj    K_r

W równaniu tym zmiennymi zależnymi od temperatury są: P. U be, Icbo i Rt, czyli:

Ic = Ic (P. U uf., Icbo, Rt)

Zgodnie z zaleceniem przedstawionym we Wprowadzeniu jako druga metoda postępowania obliczamy zatem cztery pochodne cząstkowe wyrażonej równaniem (2.10.2) funkcji dla wymienionych zmiennych (i ich wartości w temperaturze To):

Mę _ U ZAS    ,,

ÓP /?,    *

1_ _1

_k Rto _;

+ h™ =    - 0.5 V(—— + —) +100 n A = 100,1 pA

iom

10 kX2 lkfi

=-P (—+J_) = _ 100 (—!—+—) = -110 mS

ÓU„

ól_c

R, R_r =-/? + l = 100+I =101

10kf2 lkfl

ÓJ_C P-U,_E 100 0,5 V

SRt Rh

10⁶Q‘

0,05

mA

~Q

Przechodząc do skończonych przyrostów uzyskujemy wyrażenie na przyrost prądu kolektora:

ai, = *LaI,₊J^av_{u +}^ai„₀Ar_t

d\J gg    Ol r#it    oł\_r

(2.10.3)

SU_H,    Sl_Cfm ^ SR, '

Przyrównując ostatnie równanie do zera otrzymujemy zależność określającą przyrost rezystancji /łflr potrzebny do spełnienia tego warunku:

AI_C = 100,1 pA AP -110 mS■ AU_BK +101 • A1_CJW + 0,05^d/?_r = 0    (2.10.4)

AR_r =

-100,1 pA A(3-fll0mS-At/_ag-l01 A/_c

0,05

mA

"Q

czyli

AR_t = a ■ AT • R_to = -2,002 QAp + 2,2-AU _BK-2020—-• AI_CB0    (2.10.5)

mA    mA

Wartość liczbową temperaturowego współczynnika zmian rezystancji a otrzymamy podstawiając w równaniu (2.10.5) przyrosty Ap. AU be i AIcbo odpowiadające np. przyrostowi temperatur)¹ o 10 K, czyli:

AP = 10% -100 = 10: AUbf. = - 2,5 mV / K ■ 10 K = - 25 mV; AIcbo = 100 nA

AR_t = a - 10K. lkfi = - 2,002 Q 10 - 2.2—25mV + 2020-^- 100 nA (2.10.6)

mA    mA

Skąd otrzymujemy:

ARj. = al0K-lkft = - 20,02    - 55,0ft-0.2 Ś2 = -75,22    , oraz

AR_r -75,22 n ^a AT R_t,~ IOK

= —7,5-10“³ — lkfi    K

Należy zwrócić uwagę, że zmiany temperaturowe wszystkich trzech parametrów działają w tym samym kierunku, przy czym najsilniejszy jest wpływ zmiany Ubf.. Chcąc utrzymać stały prąd /<-= lOmA należałoby w miejsce Rt wstawić rezystor o współczynniku temperaturowym -7.5 • 10'* (1 / K).

Warto wspomnieć, że dla spadku temperatury o 10 K otrzymalibyśmy wynik bardzo podobny, tzn. pożądany byłby wtedy przyrost rezystancji Rt o około 75 Q. Jedyna różnica polegałaby na tym, że w obliczeniach należałoby uwzględnić przyrost AIcbo który byłby dwukrotnie mniejszy' (tzn. AIcbo = - 50 nA) niż powyżej obliczony dla przyrostu o 10 K, gdyż prąd zerowy zmniejszyłby się dla tej temperatury o połowę. Na szczęście ten nieliniowy' składnik pochodzący od zmiany prądu zerowego nie wpływa zbyt silnie na uzyskany wynik.

Niewielka nieliniowość wynikająca z wykładniczej zależności Ięao od temperatury nic ma zatem znaczenia, gdyż jest znacznie mniejsza niż błędy wynikające z zastosowanych uproszczeń i tolerancji parametrów wykorzystanych w praktycznym układzie elementów. Wystąpiłaby ona wyraźniej w wyższych temperaturach, w których składnik pochodzący od AIcbo zaczyna dominować.

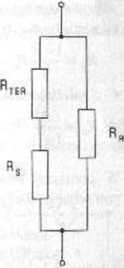
Rys. 2.10.2 (2.10.7)

(2.10.R)

Ad 2. Rozpocznijmy nasze rozważania od założenia, że dysponujemy np. termistorem NTC o współczynniku TWR równym «j£*=-5 % / K i rezystancji R$ = 1 kft lub większej. Potrzebna wartość współczynnika a = - 0,75 % / K jest (co do wartości bezwzględnej) kilkakrotnie mniejsza, a więc możemy ją uzyskać włączając szeregowo z termistorem jakąś rezystancję niezależną od temperatury. Wtedy jednak rezystancja całkowita będzie większa od podanej w temacie wartości w temperaturze odniesienia równej I kn, a więc konieczne będzie jeszcze jej skorygowanie przez równoległe włączenie drugiej rezystancji niezależnej od temperatury'. W ten sposób otrzymujemy więc układ szeregówo-równolcgły jak na rysunku 2.10.2 pozwalający na równoczesne spełnienie obydwu wymagań.

Dla termistora mamy:

RM + Rs) Ru ^ Rr⁺Rs

ck ⁼ *o [l⁺ aT£n ~ To )1 W temperaturze To musimy zapewnić:

—    czyli

W całym zakresie temperatur ta zależność ma postać:

_R _ R*(Rtfk+Rs)    (2.10.9)

R_rat + R_k + R_s

Różniczkując (2.10.9) z uwzględnieniem (2.10.1) i (2.10.7) otrzymujemy dla temperatury odniesienia 7V

[dTU

(2.10.10)