Elektronikawzad65

w. Ci^zymki r.l.EKTRONIKA W ZADANIACH

Czfić 2. Aiuliza wpływu Troinn temperatury dr pracę układów półprzewodnikowych

Prąd pobierany ze źródła zasilania będzie równy:

_<W,-"_DZ    15 V -6,2 V

R    lkii

= 8,8 mA

Odpowiada temu prąd diody stabilizacyjnej fa₇. = 6.8 mA i wydzielana na lej diodzie moc Pozma% = 6,8 mA • 6,2 V = 42 mW. Moc rozpraszana na rezystancji szeregowej R jest wtedy także największa i wynosi pRmax = 8,8 mA • 8.8 V = 77 mW

Na zakończenie zwróćmy uwagę na to. że oprócz wartości napięcia U be i jego współczynnika temperaturowego nic wykorzystaliśmy innych (celowo podanych w nadmiarze) danych dotyczących tranzystora. W tym układzie mają one wpływ tylko na rozpływ prądu emitera pomiędzy kolektor i bazę tranzystora, a to nie ma dla nas znaczenia.

Ad 2. Rezystancje dynamiczne r_BE i r_Dz zaznaczono na rysunku 2.13.2 linią punktową. Ze schematu wynika, że uwzględnienie rezystancji dynamicznej r_Bt mogłoby polegać na odpowiednim zmniejszeniu wyliczonej rezystancji R2 do wartości R2' takiej, żc R2 = R2 + r_B£. Natomiast uwzględnienie rezystancji dynamicznej rpz powoduje, że uzyskane powyżej wyniki są bezwartościowe. Napięcie na diodzie stabilizacyjnej Uoz. a więc i napięcie odniesienia staje się teraz zależne od napięcia zasilającego i jego pełna kompensacja temperaturowa musiałaby prowadzić do nieco innych wyników dla każdej wartości Uzas-

IIS• $1:W0&;    :uopi>i

wzrtit^npojemności. pła^gohp'.; dryft zera (zmiany ptinkiow pracy w stanic bez sygnału wejściowego) w pierwszym stopniu wzmocnienia wywołany zmianą temperatury otoczenia • pttteno>i iię ;iva; ; koIcjńć$j:6pai^^

Zadanie 2.14    l

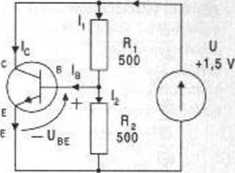
Dla tranzystora krzemowego T pracującego w stanic aktywnym w układzie jak na rysunku 2.14.1 przyjąć, że w temperaturze T₀ = 300 K:

-    spadek napięcia Use nie zależy od wartości prądu bazy Ib i wynosi 0,7 V;

-    prąd zerowy Icbo jest bardzo mały i może być pominięty;

-    współczynnik wzmocnienia prądowego w

układzie wspólnego emitera = 50.    Rys. 2.14.1

Przy zmianach temperatury otoczenia w zakresie kilkudziesięciu stopni można

przyjąć, że:

-    spadek napięcia U be maleje o 2,5 mV przy wzroście temperatury o 1 K;

-    przyrost prądu zerowego AIcbo jest bardzo mały i może być pominięty;

-    współczynnik wzmocnienia (3 przy wzroście temperatury o 1 K rośnie o I % swojej wartości w temperaturze To.

Przy powyższych założeniach należy wyznaczyć współczynnik temperaturowy napięcia zasilającego L\ przy którym prąd / pobierany z tego źródła nie zależy od temperatury.

Rozwiązanie 1

Przy oznaczeniach jak na rysunku możemy dla przyjętych założeń obliczyć wartości prądów w temperaturze T₀:

h = U_8L/R₂ = 700 mV / 500 ft = 1,4 mA, oraz /, = (U - U_BE)/Rł = (1,5 V - 0,7 V) / 500 n = 1.6 mA czyli    = /, - /₂ = 1,6 mA -1,4 mA = 0.2 mA. oraz

U: = (3 ■ I_B = 50 • 0,2 mA = 10 mA

Interesujący nas prąd I pobierany ze źródła zasilania wyraża się zależnością:

/ = /_i+/_c =

U-U_RE ]B(U-Vbe

/?, ^P

(2.14.1)

i ma wartość / = l_t + I_c = 1,6 mA +10 mA = 11,6 mA.

W tym miejscu zauważmy, żc dla stałego napięcia zasilającego U przy' wzroście temperatury wobec zmniejszania się wartości napięcia U be - prąd Ii rośnie, a h maleje. Z tych dwu powodów rośnie prąd bazy /« = //- h» a ponieważ rośnie także współczynnik wzmocnienia (3, tym silniej rośnie wartość prądu kolektora Ic. Widać więc wyraźnie, że aby prąd / = // + lc mógł przy wzroście temperatury pozostać stały, napięcie zasilające musi się zmniejszać. Poniżej spróbujemy ocenić wartość liczbową współczynnika temperaturowego tego napięcia.

W równaniu (2.14.1) zmiennymi zależnymi od temperatury są U, Ube i fi, czyli mamy:

1 = KU, Ube,P)