Elektronikawzad55

w. Ci^yiiO-i - HLKK.TRONIKA W ZADANIACH

Cxęić 2: Analiza wpływu zmian temperatury iu procę układów półprzewodnikowych

współczynnik wzmocnienia prądowego (i każdego z tranzystorów przy wzroście temperatury o 30 K zwiększy się o 30 • 0,8 % = 24 % swojej wartości początkowej, czyli o A(5= 0,24 • 99 = 24. a więc wyniesie fij = fo = 99 + 24 = 123.

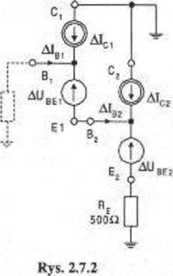
Zadaniem naszym jest obliczenie przyrostu prądu emitera AI&, gdyż od tego przyrostu zależy zmiana potencjału emitera tranzystora T2, czyli punktu pracy tego tranzystora. Schemat zastępczy układu dla przyrostów temperatury pokazuje rysunek 2.7.2.

Schemat zawiera cztery źródła wymuszające, które dla małych przyrostów temperatury traktujemy jako liniowe. Możemy więc zastosować zasadę superpozycji, czyli obliczyć prąd A/_£2 jako sumę składowych pochodzących od tych źródeł występujących osobno. Wobec tego, że rezystancja wewnętrzna źródła prądowego R, = co mamy Alm = 0. a więc AIei = Ala, a obydwa przyrosty napięcia A U be nie wymuszają żadnych prądów składowych (nic od nich nie zależy, gdyż przy rozwarciu SPM w układzie pojawia się przerwa).

Podstawiając Ais = 0 do „słusznego zawsze” wyrażenia dla stanu aktywnego (W2.7) otrzymujemy dla tranzystora Tl:

A/_C1 =(/3, +l)A/_ał01 + (/„, +W AA = A/_£, = A/,₂    (2.7.1)

Podstawiając obliczone powyżej wartości liczbowe przyrostów parametrów otrzymujemy:

M_ai =(99 + 1) 150 nA + (1 pA + lOnA) 24 = 15 gA + 24 pA = 39 pA Podstawiając powyższą wartość do (W2.7) otrzymujemy dla tranzystora T2:

A/_C2 = &A/„₂+(j8₂ +1)A/_c,_w-K/_5J + WA/3, =    (2.7.2)

= 99-39 pA + (99+1) 150 nA + (100 pA +10 nA) 24 =

= 3.86 raA -f 15 pA + 2,4 mA = 6_;27 mA Przyrost prądu emitera T2 wyniesie:

A/_£; = A/_fl2 +A/_c, = 39 p A +6,27 m A = 6,31 mA    (2.7.3)

Jest to więc poważna (63% - owa) zmiana prądu emitera. Nowa w^rartość prądu równa

16.41    mA na rezystancji emiterowej wywołuje spadek napięcia

16.41    mA 0,5 kQ = 8.2 V, tj. potencjał emitera rośnie, a napięcie Uce tranzystora T2 maleje o 3.1 V. Potwierdza się w ten sposób wniosek, że duża rezystancja w obwodzie bazy nie sprzyja stałości prądu w układzie.

W zadaniu 1.7 obliczono wartość rezystora zastępującego źródło prądowe polaryzacji bazy tranzystora Tl jako /ćj? = 8,8Mn. Dla takiego przypadku polaryzacji po znacznie bardziej skomplikowanych obliczeniach dostalibyśmy wynik nieco lepszy. Współczynnik Wr podziału rezystancji pomiędzy obwody emitera i bazy zdefiniowany dla zastępczego tranzystora (złożonego z dwu tranzystorów' Tl i T2) jak w z.adaniu 2.2 ma tutaj bardzo małą wartość:

W_K= —^-= 5710-*    (2.7.4)

R_a+R_E 8.8 MD+ 0,5 kii

ale przy bardzo dużej wartości /3 = /3; - jftr ~ 10'¹ współczynnik niestałości prądu kolektora S ma wartość mniejszą niż w przypadku polaryzacji ze źródła prądowego.

Zadanie 2.8

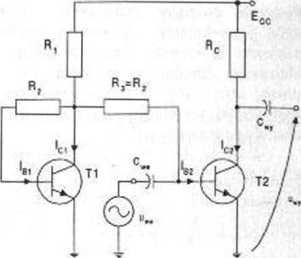
Rvs. 2.8.1

W układzie wzmacniacza prądu zmiennego jak na rysunku 2.8.1 pracują w stanie aktywnym dwa identyczne tranzystory Tl i T2, przy czym zadaniem tranzystora Tl jest stabilizacja termiczna punktu pracy tranzystora T2.

Działając na ogólnych symbolach przyrostów Aft. AU be i AIcbo jednakowych dla obydwu tranzystorów należy:

1.    wyznaczyć współczynnik niestałości temperaturowej prądu kolektora S dla tranzystora T2 zdefiniowany podobnie jak w zadaniu 2.2;

2.    przeanalizować możliwe do uzyskania wartości tego współczynnika w zależności od doboru rezystancji R/ i fo;

3.    określić, czy w tym układzie jest możliwa pełna kompensacja wpływaj zmian napięcia Ure-

Rozwiązanie

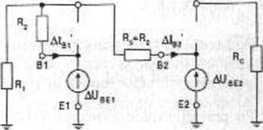
Rys. 2.8.3

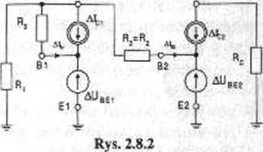
Ad 1. Schemat zastępczy analizowanego układu dla zmian temperatury przedstawia rysunek 2.8.2. Schemat zawiera cztery źródła wymuszające, które dla małych przyrostów temperatury traktujemy jako liniowe. Możemy więc zastosować zasadę superpozycji, czyli obliczyć prąd AIb każdego z tranzystorów jako sumę czterech składowych pochodzących od tych źródeł występujących osobno. Początkujący Czytelnik być może powinien dla wprawy przejść tę drogę.

Rys. 2.8.4

(2.8.1)

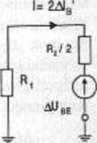
Szansę przyśpieszenia obliczeń daje nam spostrzeżenie, że rozwarcie obydwu SPM przy pozostawieniu obydwu SEM prowadzi do schematu cząstkowego jak na rysunku 2.8.3, a w tym schemacie dwie identyczne gałęzie równoległe można zastąpić dwójnikiem złożonym z SF.M i połowy rezystancji gałęzi (co pokazuje rysunek 2.8.4). po czym można już prosto obliczyć prąd płynący w obwodzie:

1££_

' RF.

l = 2Al„= —

AU„ 2-AU_H

Rt+Rj 2    2 /?,+/*,

Poszukiwane składowe przyrostu prądu bazy^- pochodzące od SEM równych AU be dla obydwu tranzystorów są sobie równe i wynoszą:

Al.. = A/,, = —

2R, +/?-.

AU,

•B7~