Elektronikawzad74

w. CUiyńakj - ELEKTRONIKA W ZADANIACH

Część 2: Analizo wpływu minii temperatury na pracę układów półptzcwx)diuitrw>xli

Dla przykładowej wartości Ri = 500 Q warunek ten jest spełniony gdyż:

Vf.cz =V_7AS-I_E2 ■ R_}-I_C1E ■ R_l = 15V-3,3V-4,9V =6,8V

W temperaturze 7” = 310 K. parametry zależne od temperatury uzyskują wartości: U be' = 600mV- 2,5 (mV / K) • 10 K = 575 mV,

/%’ = 49+ 10% -49 = 53,9 oraz Unz = 3,30 V - 1 (mV / K) • 10 K = 3,29 V.

Podstawiając te wartości do zależności (2.19.1) (2.19.3) mamy kolejno:

I _ V FFi ⁺Vpz VEB2

¹ v> ~    Z

- = 9,970mA

(2.19.1’)

(2.19.2’)

(2.19.3’)

0,5V + 3,29V-0,5V

330 n

= 0.l82mA

9,970mA

ft+l 53,9+1 1_C2 = h = Pz'1'az =53,9-0,182mA =9,788mA Tak więc „przyrost” prądu wyjściowego jest ujemny i wynosi:

A l_L = f_L-I_L = 9,788mA-9.800 mA = -12pA Odpowiadają temu następujące wartości współczynnika temperaturowego:

A/^-l^    PĄ

AT 10 K    K.    ^J

Al, _    -12pA

1_L AT ~ 9800pAIOK

= -122

ppm

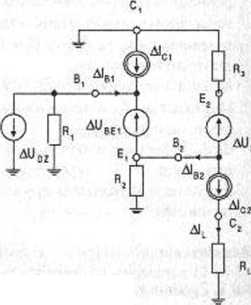
Rys. 2.19.2

i dokonując

Ad 2. Jak wynika z zależności (1.19.1) w omawianym układzie następuje kompensacja wartości napięć baza-cmilcr obydwu tranzystorów (o przeciwnym typie przewodnictwa). Dobre wyniki uzyskamy w rzeczywistości, jeśli uda się zapewnić równość współczynników temperaturowych tych napięć. Jeśli dodatkowo udałoby się zastosować skompensowaną diodę Zcncra o £dz = 0, to jak łatwo można stwierdzić na podstawie (2.19.1) uzyskujemy niezmienny prąd emitera /«. Wtedy zmiany prądu kolektora są bardzo małe i równe liczbowo zmianom prądu bazy. Na pytanie przy jakim £d7. uzyskalibyśmy niezmienność prądu kolektora można odpowiedzieć wykonując obliczenia przedstawioną metodą dla kilku przykładowych wartości interpolacji.

My jednak zastosujemy metodę schematu zastępczego dla przyrostów temperatury. Schemat ten dla analizowanego układu jest przedstawiony na rysunku 2.19.2. Na jego podstawie można napisać wyrażenia:

- AU_{nFl    (2 J9 4)}

Vmz“L

Rr

-ML-AI_Ci + A!_C2

(2.19.5)

A /    - ~ *^UFJt2 + *V»Z + A^ggl ^

--Z--

^Ki

Ponieważ w potrzebnym nam wyrażeniu (2.19.5) zmienna Ala nie występuje (nie wpływa na AI_B2, gdyż jest na schemacie zwierana przez zerową rezystancję SEM równej AUqz) nic będziemy zajmowali się w dalszym ciągu przyrostami A/_Dl i Ala-Dla tranzystora T2 wyrażenie (W2.7) (bez uwzględnienia wpływu przyrostu prądu zerowego) przyjmuje postać:

AI_C1 = I₈₂ • Aft + & • AI_Bi    (2.19.6)

Podstawiając do powyższego wyrażenie (2.19.5) otrzymujemy:

A/_Cł = /,_: A& + 0,

— - A/,

(2.19.7)

(2.19.8)

M^P₂)=l_ai -A& + ft .AOmlWi* ⁺*^u™

Al

Zakładając zJC-fo/ -/UJfjh mamy ostatecznie:

P

^A/CJ P,+l^/#2 Pj+I Ry

AU_IU _ 0,1 49

49 + 1

₀,2mA-^.^i^ (2.79.9)

49+1

330 fi

4.9    49 10mV

A/_r,=— 0.2 mA——— = 19,6 pA-29,7 pA = -10.1pA ^C2 50    50 3300    ^    ^

Jest to wynik zbliżony do obliczonego w rozwiązaniu 1 przyrostu wynoszącego ok. 12 pA, chociaż różnica jest w^r tym przypadku dość znaczna, bo wynosi prawie 20 %.

7 równania (2.19.9) można określić przyrost napięcia AUoz i współczynnik temperaturowy toz potrzebny do uzyskania pełnej kompensacji zmian prądu wyjściowego źródła (czyli Alęi - 0) dla temperatur bliskich T₀:

0.2 mA = -330 fi 20 pA = - 6.6 mV

MJ_DZ    =-330Q-5^

’    49

_R =_!!* 330fiO,2mA=-330Q-2^- = -0,66—