Elektronikawzad45

w Ciitfyń&ki - ELEKTRONIKA W 7ADANIACH

Część 2: Analiza wpływu zmian lonpcrabny na pracę układów półprzewodnikowych

330-300

•2 ^w = 2⁴ • /,

^ch 0(33oi ^— *ewx300)

cmooo)

= l60,lpA = l,6pA,

co oznacza, żc jego przerost \v>'niesic: zl/cao = 1,5 pA

- współczynnik wzmocnienia prądowego /3 przy wzroście temperatury o 30 K wzrośnie o 30 % swojej wartości początkowej, czyli o A{$ = 0,30 • 50 = 15, a więc wyniesie Pjjo= Pjoo + Ap= 50 + 15 = 65.

Podstawiając nowe wartości zmiennych P, Ubr i Icbo do wyrażeń na prądy bazy i kolektora otrzymamy:

h = (Ecc ~ U_Br)/Rb = (10 - 0,525) V f 9,4 kfl = I ,008 m A ^ _{£ p A fc — P Ib + fceo ⁼ /?/& + (/?+/) Icbo ⁼ 65 • 1,008 mA + 66 - 100 nA = 65,53 inA Prąd kolektora wzrósł o 15,53 mA, tzn. o ok. 31%. Współczynnik temperaturowy zmian tego prądu wynosi więc około 1 % / K. Wobec tego. że zmiana prądu bazy jest niewielka (poniżej 1% dla przyrostu temperatury o 30 K) możemy stwierdzić, żc główną przyczyną niestałości prądu kolektora, a więc punktu pracy tranzystora w tym układzie jest zmiana wartości współczynnika wzmocnienia prądowego /?.

Napięcie Uce*' temperaturze To wynoszące 5 V zmniejszyło się do wartości:

Ucf. - Ecc - h ‘Re = 10 V-65,53 mA • 100Q = 3,447 V czyli o ponad 1,5 V.

Ad 3. Ze zmiany napięcia Uce w punkcie pracy wynika, że w wyższej temperaturze zmniejszy się także obliczona w zadaniu 1.1 jako równa 4,4 V maksymalna amplituda niezniekształconego napięcia wyjściowego. Przy wysterowaniu wzmacniacza napięciem zmiennym bez wchodzenia tranzystora w stan nasycenia (obszar nieliniowych charakterystyk) napięcie Uce może się teraz zmniejszyć tylko o:

Uce ~ Ucej. ⁼ 3,447 V — 0,6 V = 2,85 V

Tyle też wynosi maksymalna możliwa do uzyskania w temperaturze 330 K amplituda niezniekształconego napięcia wyjściowego, przy czym przy zwiększaniu amplitudy sygnału będą zniekształcane wcześniej ujemne połówki sygnału wyjściowego.

Rozwiązanie 2 (Paniny I i 3 Jat w    !j

Ad 2. Łącząc zc sobą dwa pierwsze równania z rozwiązania 1 mamy:

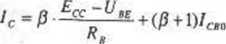
W tym równaniu zmiennymi zależnymi od temperatury są/?, U be i Icbo, czyli mamy:

lc-lc(P. U BE, IcBo)

Dla tej funkcji trzech zmiennych obliczamy pochodne cząstkowe :

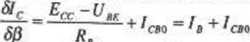
*c_Ecc-l

W r_b

*c _ P

SU ar. R_B

i przechodząc do skończonych przyrostów otrzymujemy:

Ac _A, _

- W»+- 4-w„ +(fl + itf_M

Ab

Do tego równania możemy podstawić wszystkie wartości przyrostów A/J, A6V?e i A/cflo obliczone w punkcie 2 rozwiązania 1. Otrzymamy wtedy:

A/c=(1mA + 100nA)15 + —^—75mV + 5M.5 pA = ^c    9,4ki2    (2.1.3)

= (15,001 + 0,399 + 0.077) m A = 15,47 mA

Jest to wynik bard20 bliski wartości 15,53 mA uzyskanej w rozwiązaniu l. Ostatnie równanie (2.1.3) pozwała na zorientowanie się, że zmiany wszystkich trzech zależnych od temperatury parametrów tranzystora prowadzą do wzrostu prądu kolektora (określającego punkt pracy tranzystora). Pozwala także na stwierdzenie jaki jest udział poszczególnych zmian w całkowitym przyroście Ale-

Rozwiązanie 3 (Punkty I i 3jakw rozwiązaniu I)

Ad 2. Schemat zastępczy analizowanego układu dla przyrostów temperatury pokazano na rysunku 2.1.2. Powstał on przez zastosowanie omówionego we Wprowadzeniu schematu zastępczego dla tranzystora npn. Ponieważ w temacie zadania nie mówi się o tym, żeby napięcie zasilające miało się zmieniać z temperaturą, przyjmujemy AEcc = 0, a to oznacza że końce rezystorów Rn i Rc podłączone do napięcia zasilającego, na schemacie zastępczym dla przyrostów    temperatury    okazują się

podłączone do potencjału zerowego. Schemat zastępczy zawiera dwa źródła wymuszające, które dla małych przyrostów temperatury traktujemy

jako liniowe. Możemy więc zastosować zasadę superpozycji, czyli obliczyć prąd Alg jako sumę dwu składowych pochodzących od tych dwu źródeł występujących osobno. Przypomnijmy, że składową Aln' prądu pochodzącą od SEM równej AUbe liczymy przy rozwartej SPM (patrz rys.

2.1.3) , czyli otrzymujemy:

Natomiast prąd Aln” pochodzący od SPM równej Ale liczymy przy zwartej SEM (patrz rysunek

2.1.4) . Widać wyraźnie, że cały prąd Ale płynie przez to zwarcie, C2yli mamy A Ib" = 0. lak więc sumaryczny przyrost prądu bazy wynosi:

AU_be

Rys. 2.1.2

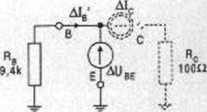
Rys. 2.13

^Rc

ioon

A/=A I„ + A1_B = —

(2.1.4)