Elektronikawzad69

w. Ciąłyńiki ELEKTRONIKA W ZADANIACH

CiikH 2; Analiza wpływu zmian temperatury na pracę układów półprzewodnikowych

^uwr = ^U7AS - ^!ci ■ ^RC2 =^{10 v} "W pA • 50 kn = 5.050 V Zauważmy jeszcze tylko w tym miejscu, że w powyższych zależnościach nic występuje wartość spadku napięcia na złączu baza-cmitcr.

Ad 2. Dla temperatury otoczenia zwiększonej o 30 °C do wykorzystanych powyżej zależności należy podstawić obowiązujące wtedy nowe wartości:

-    prądu źródła, dla którego mamy:

AJ = E-AT / =2-10^_s— 30K 200pA = l2pA K

/'= / + AJ = 200 uA + 12pA=212pA,a prądy emiterów wynoszą po 106 pA: prądu zerowego tranzystora:

Icbo’ = Icbo + AIcbo = 1 nA + 15 nA = 16 nA

-    wzmocnienia prądowego tranzystora:

=    + 40 = 99 + 30 = 129

I tak mamy kolejno:

— 16 n A = 799 nA

_/__₇    212 pA

2(fi +1) ^cao 2(129+1)

~ P    + ^Vcao “ J‘j ⁺ Icao

16 nA «105,2 pA

212pA    129

2    129 + 1

U_m =U_ząs-I_C2R_C2 = ! 0 V -105.2 pA • 50 kto = 10 V -5,259 V = 4,741 V

6000

co oznacza, że w podwyższonej temperaturze prąd kolektora każdego z tranzystorów rośnie o 6,2 pA, a napięcie wyjściowe zmniejsza się o 309 mV.

Rozwiązanie 2

Rys 2.16.3

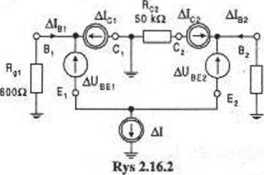
Ad 2. Schemat zastępczy rozpatrywanego układu dla przyrostów temperatury przedstawia rysunek 2.16.2. Dla małych przyrostów możemy ten schemat uważać za liniowy i na podstawie zasady superpozycji obliczyć kolejne składowe prądów bazy pochodzące od poszczególnych wymuszeń. 1 tak dla działających obydwu SEM (przy rozwartych SPM jak na schemacie cząstkowym z rysunku 2.16.3, gdzie są one przedstawione , linią przerywaną) mamy:

_A,_{ii =} Wni

_ML ₌ .

■AU,

(2.16.2)

Te składowe prądów' baz obydwu tranzystorów są równe zeru wobec tego, że tranzystory znajdują się w jednakowej temperaturze i mają jednakowe współczynniki temperaturowe zmian napięcia Cbe- Potwierdza się w ten sposób wniosek z rozwiązania 1 o całkowitym uniezależnieniu prądu bazy (a jak zobaczymy później także i prądu kolektora) w rozpatrywanym układzie wzmacniacza symetrycznego od

temperaturowych zmian napięcia Ube- Nawet jeśli w rzeczywistym układzie kompensacja zmian Ube obydwu tranzystorów nie jest pełna, to taki układ zapewnia zawsze lepszą stałość niż stopień na pojedynczym tranzystorze.

Zwierając jednocześnie obydwie SEM uzyskujemy schematy cząstkowe pokazane na rysunkach 2.16.4 i 2.16.5 pozwalające na obliczenie wpływu SPM równej odpowiednio Ala i Ala na prądy baz (dla każdej z tych SPM rezystory R_sl i R_g2 okazują się połączone równolegle:

^A/fll ^=AIB2

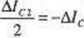
(2.16.3)

Możemy w tym miejscu założyć Ala-Ala. gdyż jak widać na schemacie zastępczym jedyna nicsymclria, tj. fakt że w tematowym układzie przyjęto Ra = 0, a Ra = 50 kCl nie ma znaczenia dla rozpływ prądu. Każdy z rezystorów Rc jest bowiem włączony szeregowo ze swoją SPM (o

nicskońezonej rezystancji wewnętrznej) i jego wartość nie wpływa na prąd w tej gałęzi.

Ostatnią składową pochodzącą od przyrostu prądu AI wyznaczamy ze schematu cząstkowego pokazanego na rysunku 2.16.6 jako:

Al'.. - AI~_C1 =    (2.16.4)

Sumaryczne przyrosty prądów bazy obydwu tranzystorów są równe i wynoszą:

(2.16.5)

A/_t. + — ^c 2

Teraz przywołujemy wyrażenie (W2.7) słuszne dla stanu aktywnego tranzystora:

u_c = Pm;+(I_b + i_cbo)aP+{P + \)u_c*o

wiążące przyrost prądu kolektora tranzystora z jego przy czynami w postaci &P. AJb i AIcbo- Podstawiając do niego otrzymaną zależność (2.16.5) otrzymujemy wyrażenie:

AJ_c~(P + l)Al ₊ 1_CM)AP ₊ P~-P-Al_r    (2.16.6)

Po prawej stronie równania pojawi! się ze znakiem ujemnym składnik zależny od poszukiwanego prądu Ale• Po przeniesieniu na lewą stronę zwiększy on wartość współczynnika, przez który mnożony jest przyrost Ale, aby zrównoważyć sumę trzech składników pochodzących od trzech przyczyn niestałości (AIcbo, Afi i Al).