Elektronikawzad44

W. Ciązyńdci Ft.F.KT ROMKA W ZADANIACH C»f3ć 2: Analiza w-plywj zmian ccmpciaiuiy na pracę ukłir!6w półprzewodnikowych

„środkowego punktu” schematu zastępczego tranzystora, a dla tranzystora pnp mają zwroty przeciwne.

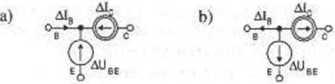
Rys. W2.4. Schematy zastępcze dla przyrostów temperatury a) tranzystora npn. b) tranzystora pnp

Sposób postępowania przy wykorzystaniu tej metody można podsumować dla najprostszych układów jak niżej:

a)    rysujemy stałoprądowy schemat zastępczy analizowanego układu dla przyrostów temperatury, uwzględniając tylko przyrosty napięć i prądów zasilających i zastępując przyrządy półprzewodnikowe omówionymi schematami elementarnymi:

b)    schemat rozwiązujemy stosując metodę superpozycji (schemat dla małych przyrostów temperatury traktujemy jako liniowy). Najczęściej w wyniku uzyskujemy zależność pomiędzy nieznanymi przyrostami prądów AIr i Ale',

c)    zależność z punktu b) w połączeniu z równaniem W2.7 tw-orzy układ 2 równali z dwoma niewiadomymi pozwalający na wyznaczenie przyrostów prądów AIr i Ale, a następnie pozostałych zmiennych określających zmiany punktów pracy przyrządów półprzewodnikowych w układzie.

Na zakończenie zwróćmy jeszcze uwagę na praktyczne aspekty' wyboru metody analizy wpływ-u temperatury' w układach półprzewodnikowych:

•    pierwsza z omawianych metod (tzn. metoda dwukrotnego obliczania punktów pracy) najczęściej okazuje się najprostsza, a wyniki uzyskane przy zastosowanych założeniach są najdokładniejsze, gdyż uwzględniają wykładniczy charakter przyrostu prądów zerowych;

•    drugą metodę zaleca się stosować w przypadku, gdy w analizowanym układzie mamy elementy, których jakichś parametr zmienia się z temperaturą według zależności określonej wzorem algebraicznym, jak np. termistor w zadaniu 2.10 lub wtedy, gdy nie potrafimy obliczyć punktu pracy (nie znamy wartości Ir w temperaturze początkowej, występującego w^re wzorze W2.7), bo np. nie znamy wartości któregoś z napięć zasilających (a tylko wiemy, jak w zadaniu 2.11 że nie zmienia się ono z temperaturą);

•    zaletą drugiej i trzeciej metody jest to, że pozw^łaląją one na ocenę znaczenia zmian poszczególnych parametrów' (np. AU be, AIcbo, Ap) dla całkowitego przesunięcia punktu pracy (zmiany wartości prądu lub napięcia stałego). Aby uzyskać takie same informacje przy użyciu pierwszej metody musielibyśmy obliczenia wykonywać kilkakrotnie, oddzielnie analizując wpływ każdego zależnego od temperatury parametru.

Część prezentowanych zadań jest rozwiązywana przy wykorzystaniu dwu lub nawet trzech omawianych metod, dzięki czemu możliwe jest porównanie przydatności tych metod i dokładności uzyskiwanych wyników.

W ostatnich dwu zadaniach wykorzystano bardziej skomplikowaną aproksymację zachowania się tranzystora przy zmianach temperatury.

w. Ci**ymWi r.I.EKTRONIKA W ZAOAWACH

C.ręić 1: .\nali7n wpływu 7mi«i temperamry nu pucę ilkUd/fo- pólpr7e\vo(fniVowych

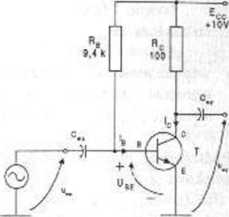
Rys. 2.1.1

Zadanie 2.1

Dla tranzystora krzemowego T pracującego w stanie aktywnym w układzie wzmacniacza ze wspólnym emiterem jak na rysunku 2.1.1 można przyjąć, że w temperaturze Tn = 300 K:

-    spadek napięcia Ube nie zależy od wartości prądu bazy Ig i wynosi 0,6 V;

-    prąd zerowy Icbo wynosi 100 nA;

-    współczynnik wzmocnienia prądowego w układzie wspólnego emitera /} = 50.

Przy zmianach temperatury otoczenia w zakresie kilkudziesięciu stopni można przyjąć, że:

-    spadek napięcia Ubf, maleje o 2,5 mV przy wzroście temperatury' o 1 K;

-    temperatura podwojenia prądu zerowego Icbo wynosi 7,5 K;

• współczynnik wzmocnienia prądowego P przy' wzroście temperatury o 1 K rośnie o 1 % swojej wartości w temperaturze To.

Przy podanych założeniach należy:

1.    wyznaczyć punkt pracy tranzystora określony przez wartości prądu kolektora Ic i napięcia kolektor - emiter Uce w temperaturze To\

2.    wyznaczyć punkt pracy tranzystora określony jw., ale w temperaturze Ti = 330 K;

3.    określić w jaki sposób przy wzroście temperatury' zmieni się maksymalna amplituda niezniekształconcgo napięcia wyjściowego.

Rozwiązanie 1

Ad 1. Analizowany układ jest identyczny z rozpatrzonym w zadaniu 1.1. Jedyna różnica polega na konieczności uwzględnienia prądu zerowego tranzystora. Dla oznaczeń jak na rysunku możemy napisać:

h = (Ecc - U_be)/R_b = (10 - 0.6) V / 9.4 kfi = I mA

Ic— P ■ Ib + Iceo⁼ P^m Ib + (P+1) Icbo= 50 - 1 mA + 51 • 100 nA =

= 50 mA + 5,1 jiA = 50 mA Uce = Ecc - h: • /?c = 10V - 50mA - 100 £2 = 5 V Uwzględnienie prądu zerowego praktycznie nie wpłynęło na uzyskane wyniki (w porównaniu z identycznym układem rozpatrywanym w zadaniu 1.1). Jest to typowe dla tranzystorów krzemowych, w których prądy zerowe są w temperaturach zbliżonych do pokojowej bardzo małe i w obliczeniach mogą być pomijane.

Ad 2. W temperaturze 7) = 330 K (57 °C):

-    przyrost napięcia U nr. wyniesie:

A U_BE = t AT= (- 2,5 mV / K) • 30 K = - 75 mV, co oznacza że napięcie U be będzie miało wartość U_BB = 600 mV - 75 mV = 525 mV

-    prąd zerowy (podwajający się przy wzroście temperatury o każde 7,5 K) osiągnie wartość: