Image45

88
Stąd
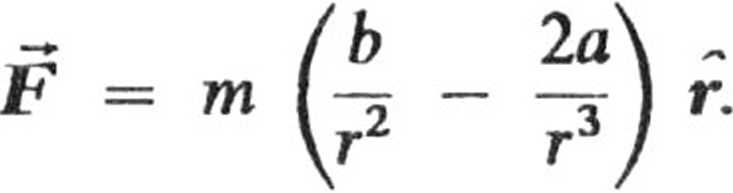
b. Z warunku
dEp
dr
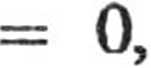
otrzymujemy
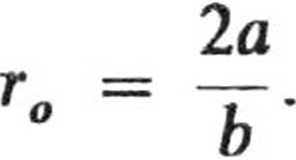
2.28
a.
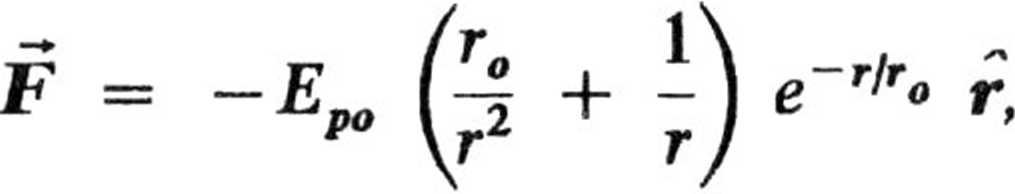
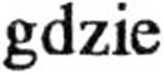
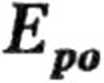
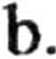
r = 6 • 1(T15 [m].
2.29.
1
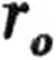
W
2.30. Pole sił jest potencjalne w przypadku a. Zatem w przypadku zadania a układ jest zachowawczy
E
Ek + E
const.
Z drugiej strony
n

0
TL
2

o
Et 1,1,- = E. (0,0,0) - ma dy + m sinz dz
2
£„(0,0,0) - m(a + 1).
. ^ •*>
o
Stąd wobec
n
Ek[ 1, 1, ^1 + 1.
= Ek (0, 0, 0) + Ev (0, 0, 0)
i
Ek(0, 0, 0) = 0,
otrzymujemy
n
2
m(a 4- 1)
2.31
a. Przyjmując początek osi x w ustalonym punkcie B, a zwrot osi zgodny z kierunkiem ruchu punktu A, otrzymujemy równanie ruchu w postaci
dv
dt
b
= — x m
Stosując podstawienie
dv
dt
= v
dv
dx
uzyskujemy po dwukrotnym scałkowaniu równania ruchu
x —
v

b
m
sin h
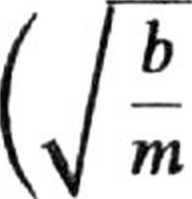
t
b. Z zasady zachowania energii
mv
2
bx
2
mv
znajduje

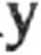
Wyszukiwarka
Podobne podstrony:
Image45 (13) 88 b. Z warunku otrzymuje; 2.28 a. m V„ 2.29. r = 6 • 1(T15 [m]. 2.30. Pole sił jest po
Strona0088 88 Porównując stosunki tych energii, otrzymujemy wartości: (3.25) —-2— V ~ A Stąd wynika
Image46 90 Stąd po rozdzieleniu zmiennych i scałkowaniu, otrzymujemy 90 b m t ln b m V o X + x2
MATEMATYKA171 332 VI Ciągi i szeregi funkcyjne Stąd dla x€<-x,x> otrzymujemy n O 21x,= *+^2^«
179 2 Ostatecznie, po wykorzystaniu warunku równowagi fazowej, otrzymuje się, że 2886 - 1,991 ■ 10&q
Z warunku x2 + y2 = 1 otrzymujemy yx 2 = ± . 1 - -t2 dla x € [-1,1 J Obliczmy wartość funkcji/dla pu
Z warunku x2 + y2 = 1 otrzymujemy yx 2 = ± . 1 - -t2 dla x € [-1,1 J Obliczmy wartość funkcji/dla pu
179 2 Ostatecznie, po wykorzystaniu warunku równowagi fazowej, otrzymuje się, że 2886 - 1,991 ■ 10&q
74113 s 206 7. Ruch pianki więc 2 3a W ~ 2b Z warunku rzutów na oś y dostaniemy aa cos 30° = stąd S
Forma i warunki zaliczenia ■ dr hab. Mirosław Tyrka prof. A Obecność studenta na zajęciach, wszystki
więcej podobnych podstron