Image46

90

Stąd po rozdzieleniu zmiennych i scałkowaniu, otrzymujemy

90

b

m

t

ln

b

m

V

o

X +

x² +

V

b/m

i po przekształceniach

v

b

m

sin/i

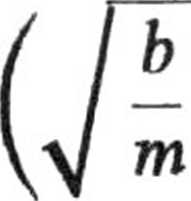
t

2.32

a. Korzystając z zasady zachowania energii

- m )    + E_p(x)

2

dt

= E,

gdzie

EAx) = m V(x) = m /I

mamy

v

dx

dt

m

(E

2

Z równania tego wynika, że przy E = m A | x , czyli w punktach

E

X j 2 — i T »

cząstka spoczywa (v = 0), natomiast w punkcie x = 0 jej prędkość staje się maksymalna

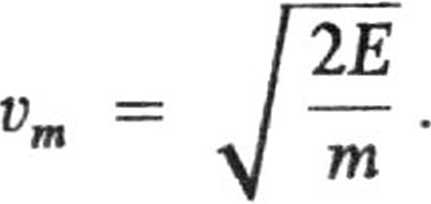
dla    x > O

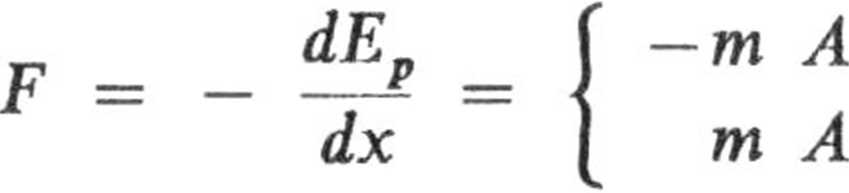
Siła działająca na cząstkę

dla    x < O

Ruch cząstki będzie więc ruchem oscylującym pomiędzy punktami x_i i x₂ Okres T oscylacji znajdujemy z równania określającego prędkość cząstki

b. Postępując podobnie jak w części a, otrzymujemy: wartość prędkości cząstki

v =

2

m

IE

m A tg²(ax)],

współrzędne punktów, w których cząstka spoczywa

i. 2

a ^arct® \l mA

wartość siły działającej na cząstkę

F

— ImaA [1 + tg²(ax)] tg(ax),

okres oscylacji

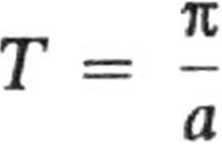
E 4- mA

Im