Image46 (13)

90

Stąd po rozdzieleniu zmiennych i scałkowaniu, otrzymujemy

90

t

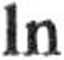
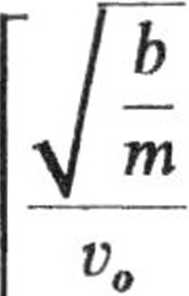
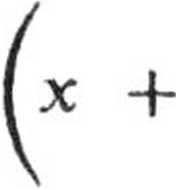
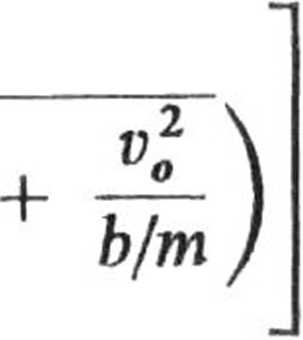
i po przekształceniach

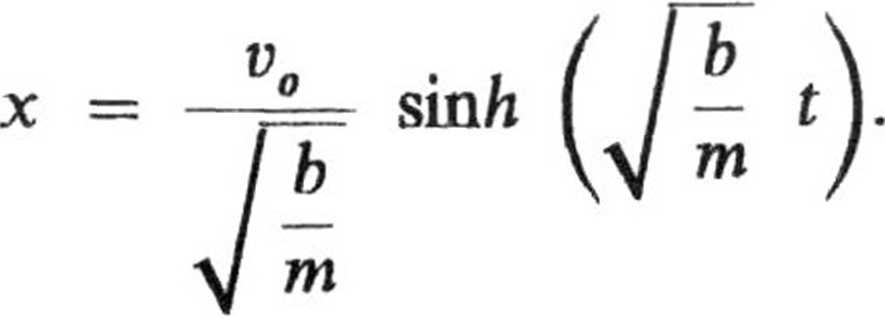
2.32

a. Korzystając z zasady zachowania energii

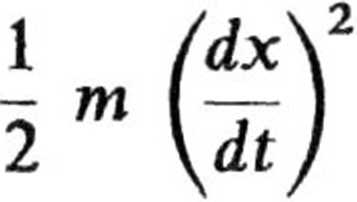
+ E_p(x) = E,

gdzie

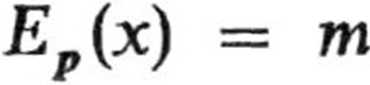
V(x) = m A

mamy

Z równania tego wynika, że przy E = m A x I, czyli w punktach

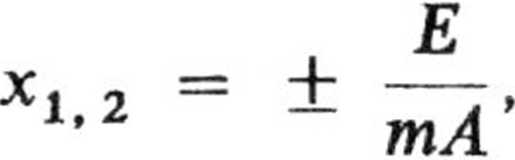
cząstka spoczywa (v maksymalna

= 0), natomiast w punkcie x = 0 jej prędkość staje się

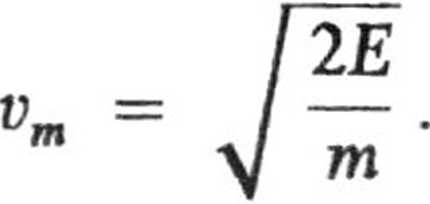
Siła działająca na cząstkę

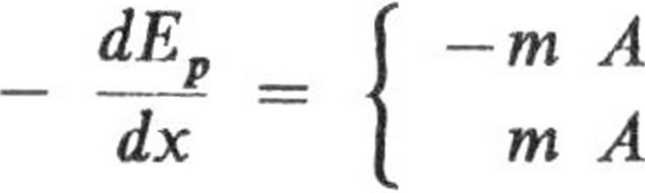
dla    x > O

dla    x < O

Ruch cząstki będzie więc ruchem oscylującym pomiędzy punktami x_t i x₂ Okres T oscylacji znajdujemy z równania określającego prędkość cząstki

II

b. Postępując podobnie jak w części a, otrzymuje

wartość prędkości cząstki

v = J^[E-mA tg²(ax)],

-    współrzędne punktów, w których cząstka spoczywa

-    wartość siły działającej na cząstkę

F = —ImaA [1 + tg²(ax)] tg(ax),

okres oscylacji

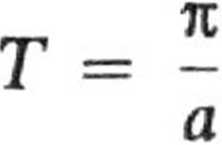
E 4- mA "

Im

«