24 luty 07 (99)

stąd po rozdzieleniu zmiennych

(O    > t

jdco = — j[M_c(t)-M_b(t)]dt    (3.141)

OJ₀    ^zr t₀

lub

₁ t

tD=a>o + — j[M_c(t)-M_b(t)'\0t    (3.142)

^Jzrt₀

Przypadek D

Analityczne scałkowanie równań ruchu nie nastręcza również żadnych problemów w przypadku D, gdy M_c - const, M_b = const oraz J_zr = const.

W innych bardziej ogólnych przypadkach rozwiązanie równań dynamicznych ruchu wymaga na ogół stosowania metod numerycznych.

Obecnie przedstawimy przykłady całkowania równań ruchu maszyny metodami analitycznymi.

Przykład 3.30

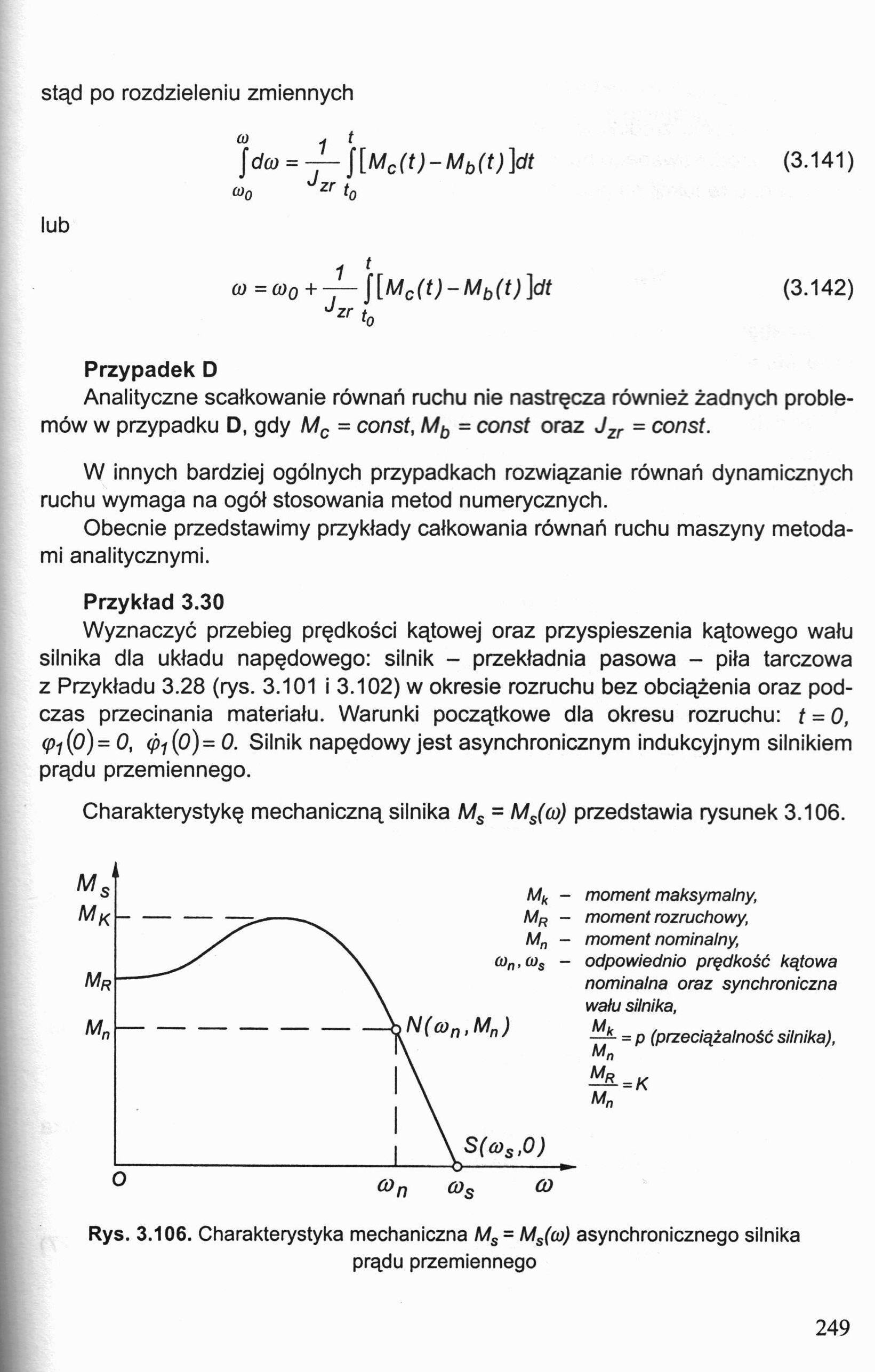
Wyznaczyć przebieg prędkości kątowej oraz przyspieszenia kątowego wału silnika dla układu napędowego: silnik - przekładnia pasowa - piła tarczowa z Przykładu 3.28 (rys. 3.101 i 3.102) w okresie rozruchu bez obciążenia oraz podczas przecinania materiału. Warunki początkowe dla okresu rozruchu: t = 0, (Pi (o) = 0, (p-i (0)= 0. Silnik napędowy jest asynchronicznym indukcyjnym silnikiem prądu przemiennego.

Charakterystykę mechaniczną silnika M_s = M_s(a>) przedstawia rysunek 3.106.

moment maksymalny, moment rozruchowy, moment nominalny, odpowiednio prędkość kątowa nominalna oraz synchroniczna walu silnika,

— = p (przeciążalność silnika), M_n

Mr

M_n

= K

Rys. 3.106. Charakterystyka mechaniczna M_s = M_s(co) asynchronicznego silnika

prądu przemiennego

249