img035 2

• Rozwiązanie metodą analityczną

Reakcję podpory A przyjmuje się w postaci jej składowych (rys. 3-9c).

W odniesieniu do rozpatrywanej belki inożna zapisać trzy równania równowagi:

IX = H_A + Pcosa = 0,

IY = J^+Rg-Psina = 0,

IM_a = — R_s-6 + Psina-8 = 0.

Z rozwiązania tych równań otrzymuje się:

H_a = — PcosóO⁰ = -50 0,5 = -25,0 kN,

Psin 60° -8    50-0,866-8

R_b =-t-- =-7-= 57,7 kN,

o    o

V_A = Psina—R_B = 50-0,866 — 57,7 = -14,4 kN.

Znaki składowych H_A i V_A są ujemne, co oznacza, że rzeczywiste ich zwroty są przeciwne do założonych (rys. 3-9c).

Wartość reakcji R_A wynosi

Ra = Jh²a + V²a = _n/(-25,0)² + (-14,4)² = 28,9 kN.

Kąt nachylenia reakcji R_A do osi x

\y i 144

tg/? = 7777 = ^ = 0-5⁷⁷² - p = w.

\n_A\ Zj,U

Właściwe zwroty reakcji R_A i R_B podano na rys. 3-9c.

Przykład 3-8. Wyznaczyć metodą analityczną reakcję podpory A belki jednostronnie utwierdzonej, obciążonej jak na rys. 3-10. Dane: P_x = 15 kN, P₂ = 10 kN.

Równania równowagi rozpatrywanej belki:

IX = -h_a = o,

zy= v_a—p_x—p₂ = o,

IM_a = M_/1-P₁-6-P₂-3 = 0.

Z równań tych otrzymuje się:

V_A = Pi+P₂ = 15 + 10 = 25 kN,

M_a = Pj-6 + P₂-3 = 15-6+10-3 = 120 kN-m.

Zwroty składowych reakcji na rys. 3-10 są zgodne z rzeczywistymi.

Przykład 3-9. Wyznaczyć wykreślnie i analitycznie reakcje podpór ramy statycznie wyznaczalnej, obciążonej jak na rys. 3-1 la. Dane: P_x = 10 kN, a, = 0, P₂ = 20 kN, a₂ = 60°.

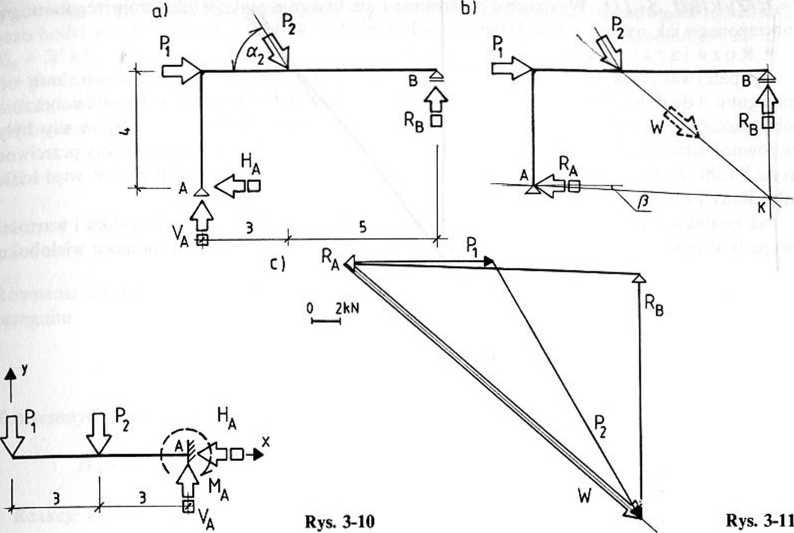
•    Rozwiązanie metodą wykreślną

Wielobok sił przedstawiono na rys. 3-1 lc. Kierunek siły W (wypadkowej sił P_l i P₂) przecina się z kierunkiem reakcji R_B w punkcie K (rys. 3-1 lb). Prosta AK wyznacza kierunek reakcji R_A (z twierdzenia o równowadze trzech sił). Ustalony kierunek tej reakcji przeniesiono na wielobok sił (rys. 3-1 lc). Wartości reakcji, odczytane z uwzględnieniem przyjętej skali sił, wynoszą: R_a = 20,0 kN, R_s = 16,5 kN.

•    Rozwiązanie metodą analityczną Równania równowagi rozpatrywanej ramy (rys. 3-1 la):

IX - -H_A + P_l + P₂cosa₂ = 0,

IY= V_A + R_B-P₂sina₂ = 0,

IM_a = -R_B'8 + P₁'4 + P₂cosa₂-4-|-P2sina₂-3 = 0.

Po podstawieniu oc₂ = 60° i rozwiązaniu równań otrzymano:

R_b = 16,5 kN, V_A = 0,82 kN, H_A = 20,0 kN.

Reakcja podpory A:

Ra = JH²a+V²a = _v/20,0² + 0,82² = 20,02 kN,

tg£ =

1^1

Wa\

0,82

200

0,041 ^P = 2°21\

55