kolo2009

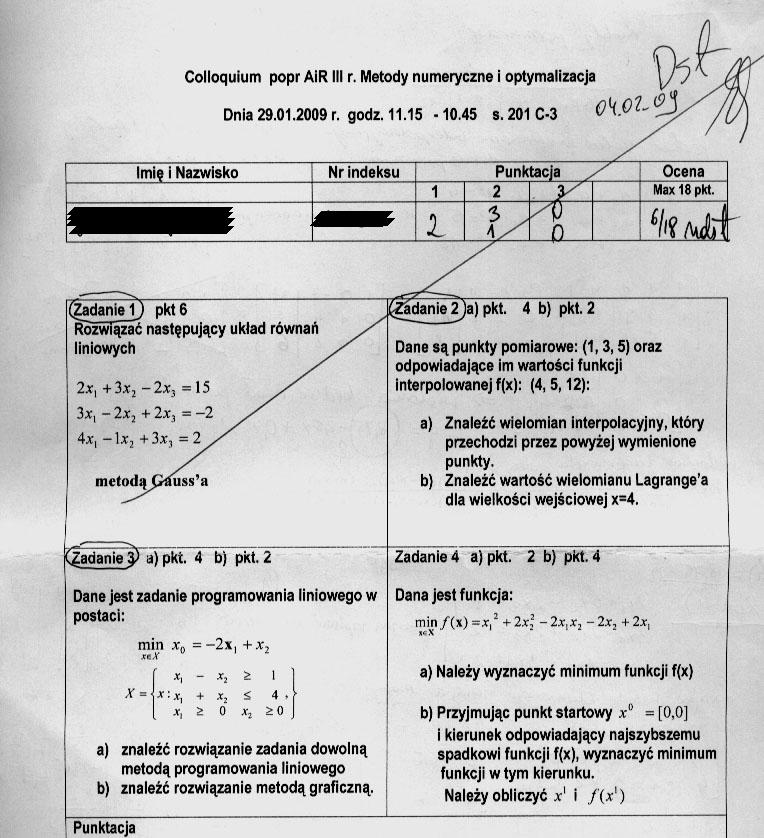
Colloquium popr AIR III r. Metody numeryczne i optymalizacja Dnia 29.01.2009 r. godz. 11.15 -10.45 S.201C-3

Imię i Nazwisko	Nr indeksu	Punk		tacja /		Ocena
		1	2			Max 18 pkt.
		1	3+	A		^ /Wid

(gadanie 1j pkt 6 Rozwiązać następujący układ równań liniowych 2.t, + 3*2 - 2x3 = 15 3x, - 2x2 + 2x3 = -2 4*, - \x2 +3x, =2 metodą Grfuss’a			(Zadanie 2ja) pkt. 4 b) pkt. 2 Dane są punkty pomiarowe: (1,3,5) oraz odpowiadające im wartości funkcji interpolowanej f(x): (4,5,12): a)    Znaleźć wielomian interpolacyjny, który przechodzi przez powyżej wymienione punkty. b)    Znaleźć wartość wielomianu Lagrange’a dla wielkości wejściowej x=4.
gadanie a) pkt. 4 b) pkt. 2			Zadanie 4 a) pkt. 2 b) pkt. 4
Dane jest zadanie programowania liniowego w			Dana jest funkcja:
postaci:			min/(x)=x,^2 +2x2^2 - 2x:x2 -2x, + 2x{
min x0 = -2x, +x2 xtX
	X{ - x2 fi! 1		a) Należy wyznaczyć minimum funkcji f(x)
X =	x’-x} + x2 £ 4 ♦
	.v, £ 0 x2 >0		b) Przyjmując punkt startowy x° = [0,0]
			i kierunek odpowiadający najszybszemu
a) znalezc rozwiązanie zadania dowolną			spadkowi funkcji f(x), wyznaczyć minimum
metodą programowania liniowego			funkcji w tym kierunku.
b) znaleźć rozwiązanie metodą graficzną.			Należy obliczyć x' i /(*’)
Punktacja