Kratownica płaska

gdzie:

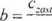
v

m

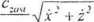
m

Korzystając z (10.20) otrzymamy układ równań różniczkowych typu (10.5) nadających się do rozwiązania numerycznego:

x, = 1, x, = x

X, ~ X

Xj = - b-Xj,

= -bx_} -g,

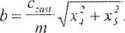
(10.25)

10.4. PRZEBIEG ĆWICZENIA

a)    Przygotować dane do programu, którymi są:

® prędkość początkowa [m/sj,

® kąt rzutu a [°j,

® zastępczy współczynnik oporu powietrza c_:as, [kg/mj.

b)    Przygotować trzy warianty obliczeń w następujący sposób: dowolne dwie z powyższych wielkości w każdym wariancie obliczeń mają być stale, natomiast trzecia będzie zmieniana.

c)    Wykonać trzy warianty obliczeń dla przygotowanych danych.

d)    Wyniki obliczeń przedstawić w postaci graficznej na jednym wykresie.

e)    Wykonać schemat blokowy działania programu RZUT.

10.5. ZAKRES SPRAWOZDANIA

Sprawozdanie powinno zawierać:

*    cel ćwiczenia,

<* bardzo krótki opis (kilka zdań) metod Rungego-Kutty,

*    wyznaczenie składowych przyspieszenia ciała w rzucie ukośnym,

» obniżenie rzędu otrzymanych równań różniczkowych z drugiego do pierwszego, ® schemat blokowy działania programu RZUT,

*    analizę otrzymanych wyników i wnioski.

11. DOŚWIADCZALNE WYZNACZANIE SIL W PRĘTACH KRATOW NICY PŁASKIEJ

11.1. CEL ĆWICZENIA

Celem ćwiczenia jest doświadczalne wyznaczenie sil w prętach kratownicy przy zastosowaniu tensometrii elektrooporowej.

11.2. OBOWIĄZUJĄCY ZAKRES WIEDZY

Student przed przystąpieniem do ćwiczenia powinien znać następujące zagadnienia: o Założenia technicznej teorii kratownic, a Metody rozwiązywania kratownic.

11.3. WSTĘP TEORETYCZNY

Kratownice są jednym z wielu ustrojów nośnych stosowanych przy budowie obiektów technicznych, takich jak: lekkie konstrukcje dachowe, maszty, suwnice, estakady itp. W zależności od rodzaju przenoszonego obciążenia stosuje się kratownice płaskie lub przestrzenne fi Oj.

Kratownicą nazywamy układ prętów przegubowych niezmienny geometrycznie pod wpływem działania sil.

Prętem przegubowym nazywamy pręt prosty nie obciążony na długości i zamocowany końcami w przegubach.

Z warunku równowagi wynika, że w pręcie przegubowym występują tylko siły normalne. Przyjmując laką definicję kratownicy determinujemy obciążenie kratownicy i siły wewnętrzne w jej prętach. Obciążenie kratownicy może być przyłożone więc tylko w węzłach, a w prętach powstają tylko siły normalne. Przyjęcie idealnych przegubów jest pewnym uproszczeniem w stosunku do rzeczywistości, bowiem w konstrukcjach inżynierskich połączenia prętów w węzłach są wykonane za'pomocą połączeń nitowych, spawanych, śrubowych itp. Powoduje to, że w wyniku odkształceń kratownicy powstają w prętach momenty gnące, skręcające, siły poprzeczne. Dodatkowe siły wewnętrzne powstają również od ciężarów własnych prętów. Z badań doświadczalnych wiadomo jednak, że wielkości te są na ogól małe i z wystarczającym dla praktyki inżynierskiej przybliżeniem mogą być pominięte.

Założenie przegubowego połączenia prętów kratownicy znacznie upraszcza sposób wyznaczania sil wewnętrznych. Aby zrealizować założenie węzłowego charakteru obciążenia kratownicy, obciążenie zewnętrzne przekazywane jest na jej węzły za pomocą konstrukcji pośredniej. Rolę takiej konstrukcji spełnia najczęściej układ belek podłużnych i poprzecznych.

- 95 -