0035

§ 2. Całkowanie funkcji wymiernych

37

otrzymujemy układ równań

A+C= 0,

- |/2 A+B+ )/2 C+D = 0 , A- \/2B+C+ y'2D = 0, B+D-l,

skąd

A =

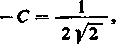
B*=D

Tak więc

J

dx

x*+i

_1_ f *+✓? _dx__L_ f *-V2—

2^2 ^J jc²+*j/T+1    2j/2 ^J x*-x]/2+\

dx =

--L—ln    ¹ +—1—arctg(x]/2+l)+—arctg^^-D+e.

4^2 jc^a—jci/^+I 2 yT    2yT

Korzystając ze wzoru na sumę arkus tangensów [50] można wynik ten napisać w postaci

—L_,_n Je!±£J^±L ₊    arc tgf^- + C

4|/2    x²-*]/2+l    2^2    1-*

Trzeba zauważyć jednak, że wyrażenie to ma sens tylko dla przedziałów (— oo, —1), (—1,1), (1, + coj*-z osobna wziętych, gdyż w punktach x = ± 1 traci ono sens. Stała C będzie dla tych przedziałów równa odpowiednio

C-

2^2

C,

c+

2/2 ’

Skokowa zmiana stałej kompensuje nieciągłość samej funkcji w punktach x = ±1.

dx.

₍₄v f 2x*-4s³+24s²-40*+20 J (*-l)(*²-2*+2)³

Uciekniemy się do wydzielania części wymiernej całki. Mamy

tak więc

Qt - (*²—2x+2)², Q_t = (*-1) (x²—2x+2) ,

2x*—4x³+24;c²—40x+20 _ ax³+bx¹+cx+d V . e , fx+g (jc—1) (je²—2x+2)³ L (jc²—2x+2)² J *-l    x²-2x+2 ’

przy czym od razu już rozkładamy na ułamki proste to wyrażenie, które podlega jeszcze całkowaniu po wydzieleniu części wymiernej całki.

Tożsamość

2x*-4x³+24x*-4Ox+20 = (3ax²+2bx+ć)(x¹-2x+2)(x-l)-(ax³+bx¹+cx+d)-2(2x-2)(x-l)+ +e(x³-2x+2)³+ifx+g) (*-l) (*²+2*+2)² prowadzi do układu równań

skąd

*⁵

**

*³

*²

x^l

x°

e+f= 0,

—a—6e—5f+g = 0, -«-2A+18e+12/-5flf = 2,

8«+2A—3c—32e—16/+12p = -4, -6a+46+5c-4rf+36e+I2/-16p =|24, —4b+id—2Ae—4f+l2g = -40, -2c-4d+ie-4g = 20,

<7-2, b - 6. c - 8. d

-9. e = 2,    /= —2,    0 = 4.