P2260011

Rozkład Gamma Gam mola. i)

Niech. X ma gęstosc zadany wzorem

fx(y) = 77777^{J    e}

i {a)

1 > 0. i > 0, jc > 0, tzn. A ma rozkład Gamma Oonuna(n. J).

M(t) E [A] Var [X ]    71    72    73    74

3°    a

($-t)^Q'    3

■foc

		r(z)= / t
		0
r(n)	= (n	-1)!
r(M	1	(2n — 1)!! _
	2 ^=
Hn + l/p)

e~* di

p_ l))fW P" J

Jeżeli A ~ F(l. i), to A ** Erp(1). Dla próby X%.....A\. ~ T(o. i).

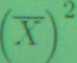
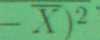
c\ 2=

ŁiW

-JL. y* Wm Z-*¹-