050

50

2. Zmienne losowe

2.4.3. Rozkład normalny

Rozkład normalny N(0,1) ma gęstość daną wzorem

/(*) =

y/2%

(2.4.6)

Rozkład

normalny

N(m,<j)

Jeśli zmienna losowa Y ma rozkład normalny N(0,1), to zmienna losowa

X — ctY + w,

(2.4.7)

Standaryzacja

gdzie o > 0, ma rozkład normalny N(m, a). W ten sposób definiuje się rozkład normalny o parametrach m i a. Z drugiej strony, jeśli X ma rozkład normalny N(m, a), co oznaczamy symbolicznie jako X ~N(m,<r), to łatwo sprawdzić, że

X =^ ~_N(0,1).    (2.4.8)

<7

Operację daną równaniem (2.4.8), odwrotną do (2.4.7), nazywa się standaryzacją zmiennej losowej X, (również w przypadku, gdy X nie ma rozkładu normalnego).

Ponieważ gęstość zmiennej losowej Y = aX + b, a > 0, gdy X ma gęstość f_x, wyraża się wzorem (patrz zadanie 2.4.10)

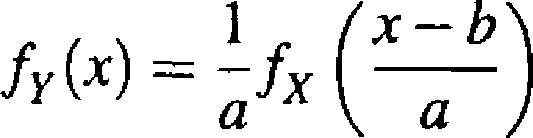
Gęstość

rozkładu

N(m,cr)

to gęstość rozkładu normalnego N(m,<7) wyraża się wzorem

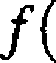
jc) = _!—e-(^JC-^m>²/²<*²    (2.4.9)

oV2n

której wykres jest przedstawiony na rysunku 6.

Wzór (2.4.9) jest bezpośrednim wnioskiem ze wzorów (2.4.7) i (2.4.6). Ponieważ gęstość f(x) rozkładu N(0,1) jest funkcją parzystą, to xf(x) jest funkcją nieparzystą, a więc dla X ~ N(m,a) otrzymujemy EX = 0, skąd ze wzorów (2.4.7) i (2.4.8) mamy EX — m. Nieco więcej zachodu wymaga obliczenie D²X. Wystarczy jednak sprawdzić, że D²X = 1, (zadanie 2.4.11), skąd od razu, ze wzoru (2.4.7) otrzymujemy, że D²X = cr².

Wniosek 2.4.1.

Rozkład normalny N(m, o) jest całkowicie opisany przez dwa parametry: m — EX i a = Vt?X.

Dystrybuantę zmiennej losowej X ~ N(0,1) oznacza się tradycyjnie symbolem <£(jt). Ponieważ dystrybuanta rozkładu normalnego nie jest funkcją elementarną, więc jej wartości trzeba odczytywać z tablic rozkładu normalnego lub