Rzuty mongea085

27

SPRAWDŹ SIĘ!

Na rys. 26abc należy odwzorować następujące proste (każdorazowo jest tylko jedno rozwiązanie):

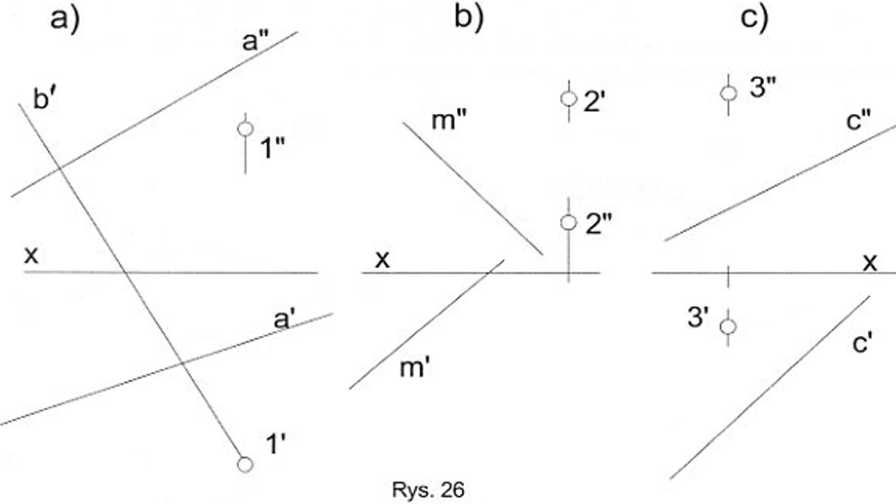
a)    skonstruować rzut pionowy (b") prostej b, która przetnie daną prostą a i przejdzie przez dany punkt 1;

b)    skonstruować rzuty prostej k. która będzie równoległa do danej prostej m i będzie przechodzić przez dany punkt 2;

c)    skonstruować rzuty prostej d - prostopadłej do tt2 i przechodzącej przez dany punkt 3; określić wzajemną widoczność prostych skośnych c i d.

3.6. Odwzorowanie płaszczyzny

Odwzorowanie płaszczyzny opisano we właściwości nr 3 rzutu równoległego (rys. 7). Wynika z niej, ze rzutem prostokątnym płaszczyzny dowolnej, czyli nieprostopadłej do rzutni, jest cała rzutnia. Dotyczy to zarówno rzutu na tui. jak i na tt:. Takie rzuty płaszczyzny trudno jest uznać za jej jednoznaczne odwzorowanie, bo nie zawieraja.. informacji o położeniu oryginału płaszczyzny w przestrzeni.

W tej sytuacji dla odwzorowania płaszczyzny dowolnej należy się posłużyć pośrednictwem zestawu takich elementów geometrycznych, które jednoznacznie płaszczyznę określają i można je jednoznacznie odwzorować, czyli zestawem złożonym z punktów i prostych.

Zestawy takie to - zamiennie wykorzystywane - trzy niewspółliniowe punkty, dwie przecinające się proste, dwie proste równoległe, prosta i nienale-żący do niej punkt.

Na rys. 7 przykładową płaszczyznę a określała trójka punktów FGH. Podobną płaszczyznę odwzorowano na rys. 27a. Trójkąt FGH jest fragmentem (wycinkiem) tej płaszczyzny.