Rzuty mongea093

35

Na rys. 33b szkicowo przedstawiono prostopadłą do m płaszczyznę cp wraz z leżącym na niej punktem P. Narysowano też prostą n - prostopadłą do płaszczyzny cp i przechodzącą przez P. W przestrzeni istnieje tylko jedna prosta n przechodząca przez P i prostopadła do cp.

35

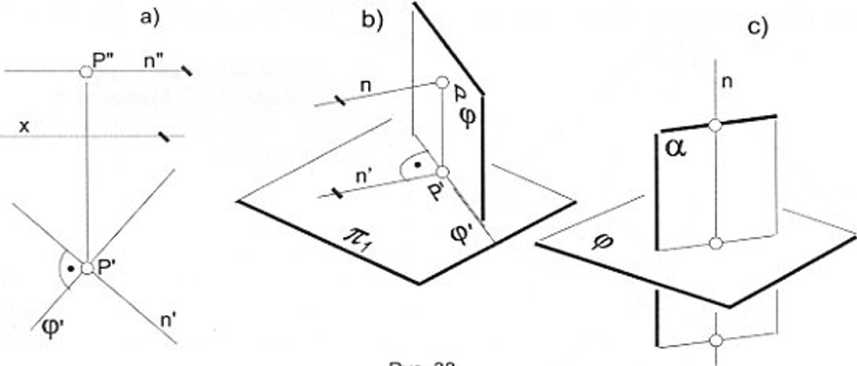
Rys. 33

Ponieważ płaszczyzna cp jest prostopadła do m, więc prostopadła do niej prosta n jest równoległa do m (zaleca się intuicyjne sprawdzenie tego na modelach: trójkąt (cp) ustawiony pionowo na blacie stołu (7Ti), ołówek (n) przystawiony prostopadle do trójkąta = równoległość ołówka do blatu stołu).

Na rys. 33a odwzorowano ten sam zestaw elementów. Równoległość prostej n do n\ oznacza, że wszystkie punkty prostej mają te same wysokości, czyli jej rzut n" jest równoległy do osi x. Rzut n' jest prostopadły do rzutu cp' płaszczyzny (wynika to z twierdzenia o rzucie kąta prostego - sprawdź na wyżej sugerowanych modelach).

4.5. Prostopadłość dwóch płaszczyzn

Twierdzenie: Jeżeli płaszczyzna a przechodzi przez prostą n, która jest prostopadła do płaszczyzny cp (szkic „przestrzenny” na rys.33c), to płaszczyzna a jest prostopadła do płaszczyzny cp.

Przykład wykorzystania tego związku zawiera rys. 34.

Dany jest tutaj trójkąt ABC, którego płaszczyzna jest prostopadła do m. Należy skonstruować rzuty prostokąta ABPQ, którego płaszczyzna będzie prostopadła do płaszczyzny trójkąta. Długości boków PQ=AB wynikają wprost z wielkości trójkąta ABC, nie narzucono konkretnej długości dla boków

BP = AQ.

Przez punkt A poprowadzono prostą n prostopadłą do płaszczyzny ABC i obrano na niej odcinek AQ o dowolnej długości. Ponieważ przez AQ (prostą n) przechodzi płaszczyzna prostokąta, a bok ten jest prostopadły do płaszczyzny trójkąta, więc (zgodnie z twierdzeniem zapisanym na początku rozdziału) płaszczyzna prostokąta jest prostopadła do płaszczyzny ABC.