Rzuty mongea120

62

b

b)

P

q

Rys. 55

7.2. Elipsa

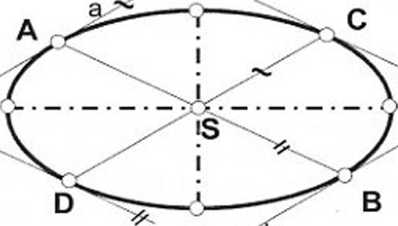
Elipsa (rys. 56a) jest krzywą c², której wszystkie punkty są punktami właściwymi. Punkt S jest jej środkiem, a każda cięciwa elipsy, która przechodzi przez S, nazywa się jej średnicą. Elipsa posiada nieskończoną liczbę średnic.

Proste styczne do elipsy, poprowadzone w punktach końcowych jednej średnicy, są do siebie równoległe (np. proste a i b w końcach A i B średnicy).

IV

I

III

b)

M

\

->> S \

\

b

N

Rys. 56

Spośród nieskończonej liczby średnic elipsy można wybrać taką (CD na rys. 56a), która jest równoległa do prostych stycznych a i b. Styczne do elipsy poprowadzone w punktach C i D są z kolei równoległe do średnicy AB. Para średnic o właściwościach takich jak AB i CD nazywa się parą średnic sprzężonych.

Elipsa jest krzywą symetryczną - środkowo (względem S) i osiowo (względem średnic). Każda ze średnic jest osią symetrii ukośnej, dla której kierunkiem symetrii jest średnica z nią sprzężona.

W jednej elipsie można wyróżnić nieskończenie wiele par średnic sprzężonych, ale dowolnie przyjętej parze połowiących się odcinków (KL i MN na rys. 56b), jako parze średnic sprzężonych, odpowie tylko jedna elipsa. A więc każde dwa dowolnej długości odcinki, przecinające się pod dowolnym kątem