Rzuty mongea091

33

a)

b)

Rys. 31

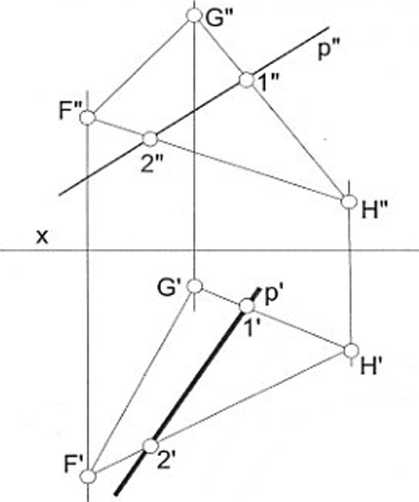
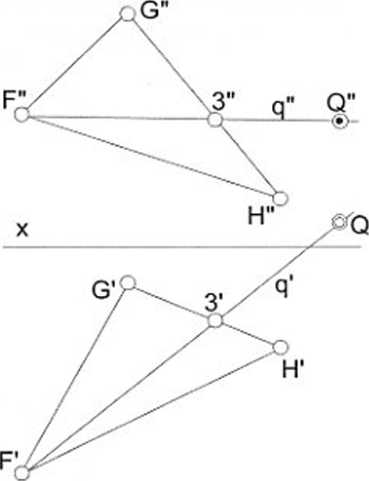
Aby zapewnić punktowi Q przynależność do płaszczyzny trójkąta FGH (rys. 31 b), należy skorzystać z pośrednictwa prostej q leżącej na tej płaszczyźnie, bowiem punkt wtedy leży na płaszczyźnie, gdy należy do prostej leżącej na tej płaszczyźnie.

Jeżeli jeden z rzutów Q został narzucony, jak np. Q" na rys. 31 b (oznaczony kółkiem z zaczernionym środkiem), to pomocniczą, prostą q należy obrać tak, żeby jej rzut q" przechodził przez Q" i przecinał dwa boki trójkąta (podobnie jak to było z prostą p na rys. 31 a). Za jeden z tych punktów na rys. 31 b obrano wierzchołek F, drugi to punkt opisany jako 3.

Ponieważ punkt Q leży na prostej q, która należy do płaszczyzny trójkąta FGH, więc Q także należy do tej płaszczyzny.

Istnieje nieskończenie wiele prostych, z których można było wybrać prostą pomocniczą q. Niezależnie od wyboru prostej pomocniczej, wynik konstrukcji (Q') będzie ten sam.

Uwaga: Na rysunku 31 b wynikowy punkt Q' (oznaczony podwójnym kółkiem) znalazł się powyżej osi x; nie świadczy to o nieprawidłowości konstrukcji, lecz jedynie o tym, że takie zadanie Q" jak na rysunku spowodowało ulokowanie punktu Q w obszarze innym niż I.

SPRAWDŹ SIĘ!

1)    W którym obszarze znalazł się wynikowy punkt Q z rys. 31 b? Odpo-wiedź poprzedź analizą znaków współrzędnych punktu Q.

2)    Na rys. 32 odwzorowano „daszek” złożony z dwóch równoległoboków o wspólnym boku AB. Na jego rzucie poziomym wykreślono wielokąt o wierz-