ScanImage49

4. Całkowanie na łańcuchach

98 h"

c

b)

V

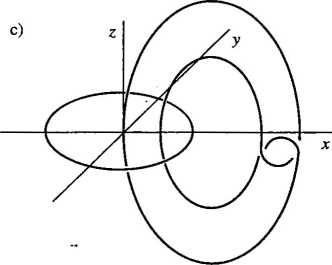
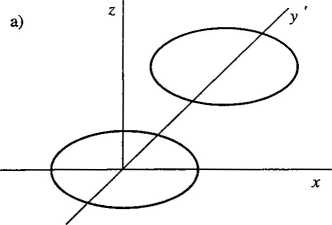
Rys. 4.6    |

Pokazać, że

3Cf,G = ^CF₀,G₀ ~ Cf,,Gi-

Cb ) Pokazać, że jeżeli    jest zamkniętą 2-formą na K³ \ 0,

/-/

^cfo>^Go

Całkowanie na rozmaitościach

Rozmaitości

Niech U i V będą zbiorami otwartymi w R". Funkcja różniczkowalna h: U —► V mająca różniczkowalną funkcję odwrotną h~^l: V -> U jest nazywana dyfeomorfizmem. (Odtąd „różniczkowalna” znaczy „klasy C°°”).

Podzbiór Mci" nazywa się k-wymiarową rozmaitością (w E"), jeżeli dla każdego punktu x e M jest spełniony następujący warunek.

(M) Istnieją zbiór otwarty U zawierający x, zbiór otwarty V c R" i dyfeomorfizm h: U -> V takie, że

h(UHM) = Vn (R^k x {0}) = {y eV: y^fc+1 = ... = /■=()}.

Innymi słowy, UHM jest równy „z dokładnością do dyfeomorfizmu” po prostu R^k x {0} (rys. 5.1).

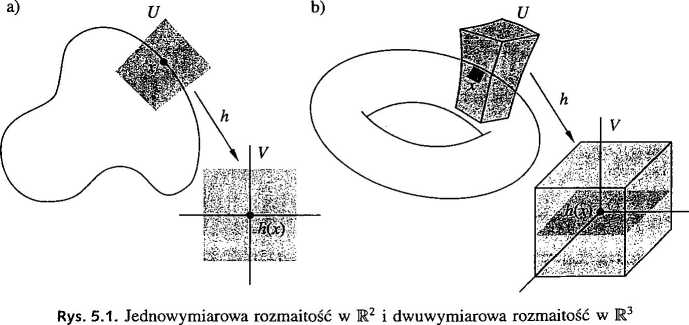
Należy zwrócić uwagę na dwa skrajne przypadki naszej definicji: punkt z R" jest 0-wymiarową rozmaitością, a podzbiór otwarty w R" jest n-wymiarową rozmaitością.

Znanym przykładem ^-wymiarowej rozmaitości jest ^-wymiarowa sfera S", określona jako {x € R"⁺¹: |jc| = 1}. To, że warunek (M) jest spełniony, pozostawiamy