ScanImage47

[ 94 h 4. Całkowanie na łańcuchach

Z drugiej strony,

J d(f dx^l A ... A dx‘ A ... A dx^k)

= J Difdx^,Adx^lA...AdxⁱA...Adx^k~ [0,1?

= (-1)'-¹ J Dif.

[0,1]*

Z twierdzenia Fubiniego i podstawowego twierdzenia analizy (jednowymiarowej) mamy

c(/ dx^l A ... A d*' a ... a z/jc*) = i    i

dx^k =

I^x

■(-l)'-¹/...(/A/(--.....

0 0 1    L    '

= (-1)'-¹ j ... j [f(x\ .... 1,    /(X¹,.... 0,..., x^k)]x

o o x duc¹... dx‘... dx^k =

= (-!)' ¹ J    1, ...,x^k)dx^l...

[0,1?

+ (-!)' J f(x¹,...,0,...,x^k)djk...dx^k.

dx^k+

[0,1]*

Tak więc

/*    3/*

CU.

Jeżeli c jest dowolną singularną fc-kostką, to zastosowanie definicji wykaże, że

c CO.

h-f

dc 3/‘

Dlatego

Jda>= J c*(dco) = J d{c*co)=c*co = J co.

c    /*    /*    3/*    3c

W końcu, jeżeli c jest k-łańcuchem Yl^ai^c.i>to mamy

*    j d co =    a,- j dco — Cli j co — /...

c    Cj    dci    3c

Twierdzenie Stokesa ma trzy nieodzowne cechy wielu najważniejszych głębokich twierdzeń:

1. Jest trywialne.

2.    Jest trywialne, ponieważ pojawiające się w nim wyrażenia zostały właściwie zdefiniowane.

3.    Ma znaczące następstwa.

Ponieważ cały ten rozdział był nieomal tylko serią definicji umożliwiających sformułowanie i dowód twierdzenia Stokesa, czytelnik powinien chętnie przyznać twierdzeniu Stokesa pierwsze dwie z tych cech. Reszta książki poświęcona jest pokazaniu trzeciej z nich.

Zadania

4.25. (Niezależność parametryzacji). Niech c będzie singularną k-kostką i niech p: [0, 1]* -* [0, 1]* będzie taką funkcją 1-1, że />([0, 1]*) = [0,1]* oraz det p'(x) > 0 dla x e [0, l]^ł. Pokazać, że jeżeli co jest k-formą, to

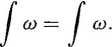
c

cop

4.26.    Pokazać, że J_Cr d& = 2tc« i wykorzystując twierdzenie Stokesa wywnioskować stąd, że c_Rjl dc dla każdego 2-łańcucha c z R² \ 0 (odwołać się do definicji c_Rn z zadania 4.23).

4.27.    Pokazać, że liczba całkowita n z zadania 4.24 jest wyznaczona jednoznacznie. Liczba ta nazywa się indeksem krzywej c względem punktu 0.

4.28.    Przypomnijmy, że zbiór liczb zespolonych C jest po prostu przestrzenią R², gdzie (a, b) = a + bi. Dla a\,... ,a_n e C określamy funkcję /: C —> C jako /(z) = z" + a\zⁿ~^x + ... + a_n. Określmy singularną 1-kostkę c_Rj: [0,1] —» C \ 0 jako c_R j — f o c«,i, a singularną 2-kostkę c jako c(s, t) — t ■ c_RtU(s) + (1 — t) ■ c_Rj(s).

(a)    Pokazać, że dc = c_Rj — c_{R n} oraz że c([0, 1] x [0, 1]) C C \ 0, jeżeli R jest dostatecznie duża.

(b)    Korzystając z zadania 4.26, udowodnić podstawowe twierdzenie algebry, każdy wielomian zⁿ + a\zⁿ~^l + ... + a_n, gdzie a_: e C, ma pierwiastek w C.

4.29.    Pokazać, że jeżeli co jest 1-formą f dx na [0, 1], gdzie /(0) = /(1), to istnieje dokładnie jedna liczba X taka, że co — Xdx = dg dla pewnej funkcji g, która spełnia S(0)=*(1).

Wskazówka. Aby znaleźć X, scałkować co — Xdx = dg na [0, 1],

4.30.    Dowieść, że jeżeli co jest zamkniętą 1-formą na R² \ 0, to co = X dd + dg dla pewnej lelig: M² \ 0 ->■ R.

Wskazówka. Pokazać, że jeżeli c_Rj *(co) = X_Rdx +d(g_R), to wszystkie liczby X_R mają tę samą wartość X.

4.31.    Pokazać, że jeżeli co ^ 0, to istnieje taki łańcuch c, że f_c co ^ 0. Wykorzystać ten fakt, twierdzenie Stokesa i własność d² = 0, aby dowieść, że d² = 0.