ScanImage46

4. Całkowanie na łańcuchach

Podstawowe twierdzenie

4

To, że zachodzi d² = 0 i 9² = 0, nie mówiąc już o graficznym podobieństwie symboli d i 3, sugeruje istnienie pewnego związku między łańcuchami a formami. Związek ten ustala całkowanie form na łańcuchach. Odtąd będziemy rozważać tylko różniczkowalne singularne «-kostki.

Jeżeli co jest k-formą na [0, 1]\ to co = f dx^l A ... a dx^k dla dokładnie jednej funkcji /. Określamy

/ / ^f-

[0,1]*    [0,1]*

Moglibyśmy także napisać to jako

J f dx^l A ... A dx^k = J f(x^l, ..., x^k)dx^l ... dx^k,

[o,i]*    [0,i]*

co jest jedną z przyczyn wprowadzenia funkcji x‘.

Jeżeli co jest k-formą na A i c jest singulamą k-kostką w A, to określamy

S-S

c co.

[0,1]*

W szczególności zauważmy, że

j

x^k)dx^l ... dx^k.

J f dxⁱ A ... A dx^k = J (I^k)*(f dx^x A ... A dx^k) == J /(;t¹,...,.

[0,1]*

[0,1]*

Dla k = 0 musimy podać odrębną definicję. Forma co rzędu 0 jest funkcją; jeżeli c: {0} -*■ A jest singulamą 0-kostką w A, to określamy

J co = tw(c(0)).

C

_ *

Całkę z co na k-łańcuchu c ~ YS ^ai Ci określamy jako

i J ^M J &¹-

C    Cj

Całka z 1-formy na 1-łańcuchu nazywana jest cz6*sto całką krzywoliniową. Jeżeli Pdx + Qdy jest 1-formą na R² oraz c: [0, 1] R² jest singulamą 1-kostką (krzywą), to można dowieść (czego nie zrobimy), że

/Tl

Pdx + Qdy = lim^c¹^) - c¹^-,)] ■ P(c(f')) + [c²(ń) - c²(r,_₁)]Q(c(fⁱ)),

gdzie to.....t_n jest podziałem odcinka [0, 1], t' jest dowolnie wybranym punktem

^z [ń -1, f(], a granicę bierze się dla wszystkich podziałów przy średnicy podziału (równej

największej z liczb |f, — f/_i|) zmierzającej do 0. Prawą stronę często przyjmuje się jako definicję całki f_c P dx + Qdy. Podejście to jest naturalne, ponieważ sumy te są bardzo podobne do sum pojawiających się w definicji zwykłej całki. Jednak takie wyrażenie jest prawie bezużyteczne przy konkretnych rachunkach i przekształcane jest szybko w całkę równoważną całce f_{[0 y]}c*(P dx + Qdy).

Analogiczne definicje dla całek powierzchniowych, to znaczy całek z 2-form na 2-kostkach singulamych, są jeszcze bardziej skomplikowane i trudne do zastosowania. Jest to jedną z przyczyn, dla których unikaliśmy takiego podejścia. Inną przyczyną jest to, że podana tu definicja zachowuje sens w przypadku ogólniejszym, rozważanym w rozdziale 5.

Związek między formami, łańcuchami oraz symbolami d i 3 jest podany krótko i najbardziej elegancko w twierdzeniu Stokesa, które czasami nazywa się podstawowym twierdzeniem analizy wielowymiarowej (jeżeli k = 1 i c = I¹, to rzeczywiście jest ono podstawowym twierdzeniem rachunku różniczkowego i całkowego).

4.13. TWIERDZENIE STOKESA. Jeżeli ca jest (k-l)-formą na zbiorze otwartym A C K" i c jest k-łańcuchem w A, to

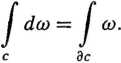
Dowód. Załóżmy najpierw, że c = /* oraz w jest (k - l)-formą na [0,1]*. Wówczas ca jest sumą (k — l)-form postaci

f dx^] A ... A dx‘ A ... A dx^k

i wystarczy dowieść twierdzenia dla każdej z nich z osobna. Wymaga to tylko rachunku. Zauważmy, że

j /&«)•(/ dx^l A ... A dx‘ A ... A dx^k) =

0,    jeżeli j / i,

J f(x^l, ...,a, ...,x^k)dx^l ...,dx^k, jeżeli j — i.

[0,1]*

Dlatego

J f dx^l A ... A dx‘ A ... A dx^k =

3/*    k    »

A ... A dx‘ A ... A dx^k) =

^J-'    mi)-'

= (-l)ⁱ⁺¹ f f(x¹,...,l,..., x^k)dx^l. ..dx^k+ [0.1]*

+ (-!)' J    o, ...,x^k)dx^[...dx .

[0,1]*