skanowanie0086 3

176 Optyka

Szerokość maksimum centralnego jest wyznaczona przez położenie pierwszego minimum (;n=l). Ze wzoru (43.4) wynika, że dla szerokich szczelin (a » A) pierwsze mirtimum pojawia się już przy bardzo małym kącie, co oznacza, że centralne maksimum jest wąskie i odwzorowuje geometryczny kształt szczeliny. Gdy szerokość szczeliny jest równa długości fali, pierwsze minimum występuje dla kąta i? = 90°, co oznacza, że centralne maksimum wypełnia całą przestrzeń za szczeliną. Jeżeli ekran w tym przypadku nie jest zbyt duży, możemy przyjąć, że jego oświetlenie jest jednorodne.

Dwie szczeliny

Obraz otrzymany na ekranie przy przechodzeniu światła przez dwie szczeliny (rys. 43.3) jest wynikiem jednoczesnego wystąpienia dwóch zjawisk: dyfrakcji światła na każdej ze szczelin oraz interferencji fal wychodzących z sąsiednich szczelin.

Maksima interferencyjne występują w punktach ekranu, dla których różnica dróg AS jest wielokrotnością długości fali. Z rysunku 43.3 widać, że AS = rfsint?, więc położenie maksimów interferencyjnych określa związek:

dsinó = mA, m-1,2,3...    (43.5)

Odległość kątowa prążków interferencyjnych jest określona przez stosunek Md, gdzie d jest odległością między środkami sąsiednich szczelin. Względne natężenie tych prążków jest określone przez obraz dyfrakcyjny pojedynczej szczeliny, a więc zależy od stosunku Ma, gdzie a jest szerokością szczeliny. Można

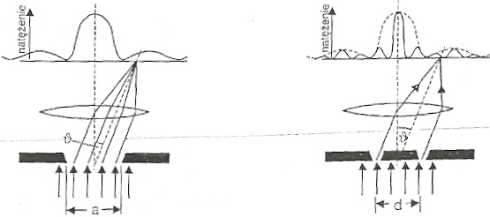
Rys. 43.2. Dyfrakcja na pojedynczej szczelinie

Rys. 43.3. Dyfrakcja na dwóch szczelinach

powiedzieć, że prążki interferencyjne mają natężenie modulowane przez dyfrakcyjną obwiednię. Gdy szczeliny są bardzo wąskie, obraz dyfrakcyjny jest bardzo szeroki - wszystkie prążki interferencyjne mają niemal takie samo natężenie i na ekranie obserwuje się tylko obraz interferencyjny.

Siatka dyfrakcyjna

Zjawiska podobne do opisanych wyżej zachodzą, gdy liczba szczelin jest większa. Taki układ równoległych szczelin, leżących w równych odległościach, nazywamy siatką dyfrakcyjną. Siatki dyfrakcyjne wykonuje się przez nacięcie rowków na szkle lub na metalowej płycie ostrzem diamentowym. Siatki szklane nazywamy transmisyjnymi, gdyż światło obserwujemy po przejściu przez szczeliny, siatki metalowe zaś nazywamy odbiciowymi, ponieważ interferencji ulegają tu promienie odbite. Sporządziwszy taką wzorcową siatkę dyfrakcyjną, można wykonać następne siatki. W tym celu wzorcową siatkę pokrywa się roztworem kolodium, a następnie zdejmuje stwardniałą powlokę i przykleja ją do płytki szklanej lub innej podkładki. Mniej dokładne siatki wykonuje się metodą fotograficzną.

W siatkach dyfrakcyjnych szerokość szczelin jest rzędu długości fali, więc natężenie prążków interferencyjnych jest prawie stale.

Zwiększenie liczby szczelin od dwóch do N nie zmienia położenia maksimów interferencyjnych, które są w dalszym ciągu opisane równaniem (43.5), lecz powoduje pewne zmiany ich kształtu. Mianowicie, ze wzrostem liczby szczelin maksima stają się coraz węższe. Szerokość kątową maksimum wyraża wzór:

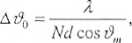
(43.6)

gdzie i9_m oznacza kąt występowania maksimum rzędu m.

Z równania (43.5) widać, że położenie maksimum zmienia się z długością fali. Ta właściwość pozwala na zastosowanie siatek dyfrakcyjnych do rozdzielania przestrzennego składowych światła złożonego, czyli do analizy widmowej.

Aby móc rozróżnić fale, których długości niewiele się różnią, maksima główne powinny być możliwie najwęższe. Zdolność rozdzielczy siatki dyfrakcyjnej definiujemy następująco:

AA

(43.7)

gdzie źl jest średnią długością fali'dwóchrliuii"widmowych ledwie rozróżnialnych, a A/łjest różnicą długości fal między nimi.

Według kryterium Rayleigha dwa maksima są ledwie rozróżnialne, gdy ich odległość kątowa jest taka, że maksimum jednej linii przypada na minimum drugiej. Jeśli zastosujemy to kryterium, to okaże się, że zdolność rozdzielcza siatki dyfrakcyjnej jest proporcjonalna do całkowitej liczby szczelin oraz do rzędu widma

R = Nm. (43.8)