skanuj0031 2

ZADANIA UZUPEŁNIAJĄCE

1.    O prostych a,b,c,d,e,f ,g ■wiadomo, że alb, b |j e, c 1| d, die, elf, f 11 g. Jak położone są względem siebie proste a i g, a jak proste c i f?

2.    Półprosta AB jest prostopadła do pół-prostej BC oraz równoległa do półpro-stej BD i do półprostej CE. Czy wynika stąd, że punkt D leży na półprostej AB? Czy odcinek DE może być prostopadły do odcinka AB ?

3. Ile wynosi suma miar kątów a i /??

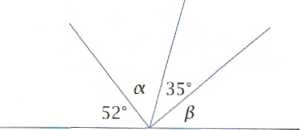
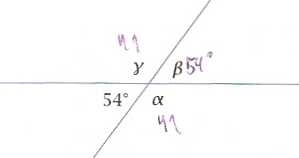
4. Jakie miary mają kąty a, fi i y?

5. Jeden z kątów trójkąta równoramiennego ma miarę 100’. Jakie są miary pozostałych kątów tego trójkąta?

^Czy trójkąt jest równoramienny, jeśli

dwa z jego kątów mają miary:

a> 65 i 50", b) 60 i 55", c) 60 i 60 ?

7.    Obwód trójkąta równoramiennego wynosi 10 cm, a jeden z jego boków ma długość 4 cm. Jakie są długości pozostałych boków?

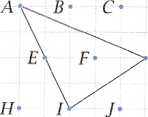
8.    Znajdź kilka trójkątów przystających do trójkąta AIG o wierzchołkach w zaznaczonych punktach.

9.    W trójkącie prostokątnym ABC kąt BAC jest prosty, a kąt ABC ma miarę 40°. W trójkącie DEF kąt przy wierzchołku D jest prosty. Uzasadnij, że aby trójkąt DEF był przystąjący do trójkąta ABC, wystarczy, że:

a)    \DF\ = |AC| i \DE\ = \AB\

b)    | <EFD\ = 50- i |£F| = |BC|

C) | <EFD| i 50“ i \DF\ = |AC|

10.    Narysuj dowolny prostokąt i połącz odcinkami środki sąsiednich boków. Jaki czworokąt otrzymałeś?

11.    Jedna z przekątnych rombu ma taką samą długość jak bok rombu. Jakie miary mają kąty tego rombu?

12.    Skonstruuj równoległobok, który nie jest prostokątem i w którym wysokości mąją długości 3 cm i 4 cm.