teoria1

LICZBY ZESPOLONE

C - zbiór liczb zespolonych

ę = {(*,

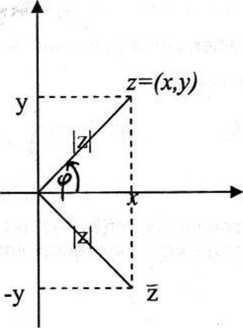
x = Re z - część rzeczywista I. zespolonej y = Im z - część urojona z = x + iy - postać algebraiczna I. zespolonej

i = (0,1), i²=-l

Działania:

(W,) + (W₂) = (*| + Wi +^2)

(Wi)-(*2.^2) = (*1*2 - y^2 >*■ yi->.*2)

|z[

- sprzężenie

Dla z₂ = 0 : nie określamy argumentu.

arg z -argument główny z:

argz = {(p € R : (p e >4rgz a ę? e< 0;2zr)}

Własności argumentu:

1.    arg(ź) = 2^-argz

2.    arg(-z) = argz + ;r dla 0 < argz < n

argz - n dla n < argz < 2;r

y i A

= -^x²+y² -moduł

3. arg

\^zJ

= 2 n- arg z

z -x-iy

- I |2

z-z = |z|

Własności modułu:

^zi|

1.		^Z2
	z.
2.		=
	^zi
3.	z,+z

Własności sprzężenia: 1. z

= r4»^z2 *0

z₂ = z,

2.

k^Z2 ^

= =»^Z2 * 0

3. Z, +Z₂ =Z, +z₂ Moduł w geometrii:

4.    argz,-z₂ = argz, + argz₂+2for k = 0v k = -\

5.    argz" = /j• argz, + IkK    ke%.

6.    arg — = arg z, - arg z₂ + 2kn

^zi

k = 0v& = -l

*w 4, 5 i 6 k należy dobrać tak, by (p €< 0;2zr)

Postać trygonometryczna liczby zespolonej: z = |z| • (cos ę + isin q>\ (pe Argz

Działania: // dla z, = |z,|-(cos^), + i-sinę^);

^ZL ~ KI' (^cos V* ^{+ 1}' ^s*ⁿ ^2 )

1.    z, • z₂ = |z, • z₂1• (cos(ę>, + <p₂) + i-sin(ęj, + ę₂))

2.    z" =|z_ir -(cosMęj, +/'Sinnę?₂)

Pierwiastki stopnia n liczby z leżą na okręgu o środku w punkcie (0,0,) i promieniu v^;|z| eR, dzieląc okrąg na n równych części.

Gdy znamy jeden z pierwiastków z₀:

.    2kn . . 2&;r

z_i=z₀-(cos-+ isin-)

n    n

Każde równanie stopnia n o zespolonych współczynnikach ma dokładnie n pierwiastków. Niech P(z) będzie wielomianem stopnia n zmiennej zespolonej o rzeczywistych współczynnikach:

P(z) = a_nzⁿ + an-tz"'¹ + ... + a₂z + a₀; a„ * 0, Vie{0,l,...,«} aieR

Wtedy P(z₀) = 0 P(z_Q) = 0 Postać wykładnicza I. zespolonej: e‘* = cosę> + /-sinę> ,

Własności:

1. z = \z\-e

,i<p

z = z • e

1 1

r«P

3. — = —e

-i<p

4. z,-z₂ = z, • z₂|-e

5. -z=z-e

<(«>+*)

+9l)

6. fL ₌

^Z2 KI

|z, - z₂1 = -/(x| - x₂ )² + (y, - J>2 )² ' odległość między punktami

|z - z₀| = r - równanie okręgu o środku w punkcie

z₀ i promieniu r

Argument liczby zespolonej:

Arg z - argument z:

Dla z₂ 0:

X    V

/lrg = {ę>:cosę> = 7-rAsinę? = i-r} z    z

Z I

3. — = J-Ą ■ (cos(p, -(p₂) + i-sinfo?, -(p₂))

z,

Wzór Moiyre^: |z| > 0 : z" = |z|ⁿ(cos«ę> + i-smn<p), gdzie n jest I. naturalną

Pierwiastkiem stopnia n liczby z nazywamy każdą liczbę zespoloną w: w"=z

- zbiór pierwiastków n-tego stopnia liczby z ; = Z, "yfz = {\V₀,W_l,W₂,...,W_k,...,W_n._[} ,

W,

w,.

= ^jz (cos

(p+lkn . . (pA-lkn

H-sin-

-)

n

n