8 (915)

Liczby zespolone

:h w postaci alge-żenie wielomianów ; zespoloną x + W, sbę x - iy, aby w

X

Re z

z~x+iy

-,ja geometryczna iczby zespolonej.

Postać algebraiczna ś sprzężenie liczby zespolonej    15

® Definicja 1.2.9 (sprzężenie liczby zespolonej)

Sprzężeniem liczby zespolonej z = x + iy, gdzie x,y G R, nazywamy liczbę z określoną wzorem:

_ def

z — x — iy.

Liczba sprzężona do liczby zespolonej jest jej obrazem w symetrii względem osi Re z (rys. 1.2.3).

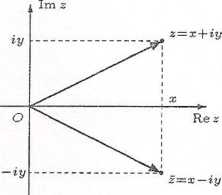
Rys. 1.2.3. Interpretacja geometryczna sprzężenia liczby zespolonej.

Ą- Im z₂;

iznej)

li części rzeczywiste i

yarunki:

1. z\ + z2 — zi + z2;	2. zi — 2
3. zi • z2 = zi • z2;	4. (-)
5. z + z = 2 Re z;	\^z2j 6. z — z
7. (z) = z;	8. Im (z

Fakt 1.2.10 (własności sprzężenia liczb zespolonych)

Niech z, z₁, z₂ € C. Wtedy

= zŁ, O ile z₂ 7^ 0;

= 2żlmz;

) = -Im(4

Uwaga. Równości podane w punktach 1. i 3. są prawdziwe także dla dowolnej

liczby odpowiednio składników i czynników.

I

O Ćwiczenie 1.2.11

Rozwiązać równania:

1a) 2z + (3 — i)z — 5 + 4i;    b) z + i — z + i\

c) z ■ z + (z — z) — 3 + 2i]    d) 2 + z + i (z — z) — 5 + 3i.

O Ćwiczenie 1.2.12

Uzasadnić podane równoważności:

a) liczba zespolona z jest liczbą rzeczywistą z — z •$=$> Im z — 0; b) liczba zespolona z 7^ 0 jest liczbą czysto urojoną -4=^ z = —z <=> Re z — 0.

O Ćwiczenie 1.2.13

Wyjaśnić, dlaczego w zbiorze liczb zespolonych nie można wprowadzić relacji nierówności (<) tak, aby zachowane były wszystkie jej własności ze zbioru liczb rzeczywistych.

(2 + 1.    ■ ^A i