0127

128

II. Funkcje jednej zmiennej

punkt jc=0 jest punktem nieciągłości drugiego rodzaju — z obu stron; mianowicie przy x-*0 jest

|/(x)|-»co:

1

/(+0)= lim -, = + 00, *-. + ox

1

/(—0)= lim -r= —co.

n-OX

4) Funkcja

(przy x^0)

1

/(x) = sin— x

rozważana w ustępie 54,9) w punkcie r=Oma nieciągłość drugiego rodzaju z obu stron, ponieważ nie istnieje żadna z granic jednostronnych tej funkcji przy jc->0.

5) Natomiast funkcja [54,10)]

/(jc)=x sin —    (przy x ź 0),

x

dla której, jak wiemy, istnieje granica

lim/(x)=0,

x -* O

może być — zgodnie z uwagą z ustępu 66 — uzupełniona do funkcji ciągłej w x = 0, przy przyjęciu

/(0)=0.

6) Określmy dwie funkcje równościami:

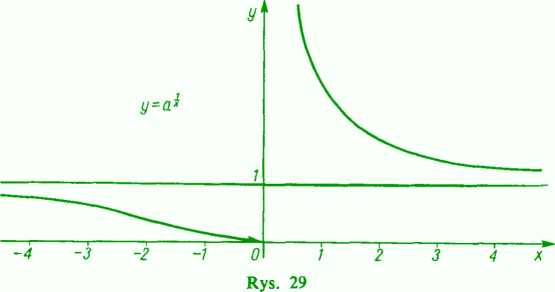
/iW=9¹¹'    (o> 1), /₂W=arctg —

x

dla X9ⁱ0, a ponadto przyjmijmy /j(0)=/₂(0)=0.

Dla pierwszej z nich mamy:

/i(+0)= lim a^llx— lim o'= + oo,

x-» + 0    z~* + oo

fi( —0) — lim a'^h= lim a = 0,

X-* —O    - 00

tak żę w punkcie *=0 jest prawostronna nieciągłość drugiego rodzaju i lewostronna ciągłość. Dla drugiej funkcji mamy

1

/z(+0)= lim arctg— = lim arctgz=^ji,

x~* + O    X z -» + 00

/l(-0)=-łK.

i w punkcie jc=0 są obustronne skoki. Wykresy tych funkcji dane są na rysunkach 29 i 30.