018 (18)

Funkcja logarytmiczna

5)    p'^p“-a    a e R_

6)    Jeśli/; e (O, l)u(l, +ce). a e R i b e R. to: log_;,(c/ • h) = \o%a + log_pb

log„^'= log,,« log, A

log a‘ = t • log//, te R log />

log b = ,    </, b. p > 0 i /; * 1 / a * l

log//

1

log h = 7-</,/>> 0 i ci * I / /> * I

log//

Definicja funkcji logarytmicznej

Funkcję J\x) log.Y. x e R . /; e (0, 1) kj (1, +cc) nazywamy funkcją logarytmiczną o podstawie /;

np.:/(.v) = log_rv,/(.v) = logi a\/(.y) - log.y

Dwie ważne własności

(wykorzystywane np. przy rozwiązywaniu nierówności logarytmicznych)

1) Jeżeli // e (0, I) to funkcja logarytmiczna /(.r) = log .v jest malejąca, tzn. dla dowolnych .v,. a\ e R,

•v, < -v_: log/, > log/,. np.:

AY

9

8 t ⁷

r»r

5 *

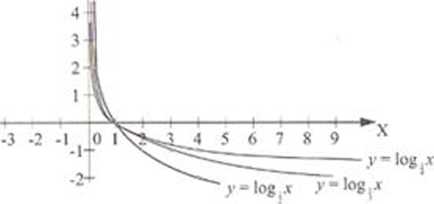
a)    f(x) = log, .v, .v e R,

*

•V = 1/(1) = logii = 0

2

-V = 2/(2) - logi2 = -1

.v = 4/(4) = logi4 = -2

2

b)    /(.v) = logi.w.Y e R

C) /(.Y) = logi.Y, .Y € R.

BO

2) Jeżelip e (l, + x) lo funkcja logarytmiczna/(a) - log v jest rosnąca, izn. dla dowolnych x_r a, e R

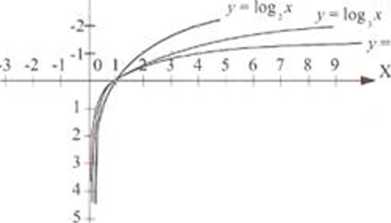
•^v, <'^v2 ° logjA, < log/2» ⁿp.:

a)    /(a) * log_r\% a* € R,

■v = 1/(1) = log, 1 = 0 a* = 2 f{2) = log,2 = 1 x = 4 /(4) = log,4 = 2

b) /(.v) = logyV, .v € R.

c) ./’(.v) = log_rv,.v € R

* Y

UWAGA!

Możesz się spotkać z następującymi oznaczeniami przy logarytmach:

Pamiętajmy, że ten zapis czytamy jako łogarytm

V = In X to jest to samo CO V = log A, A > 0 naturalny z liczby dodatniej x.

Uwaga: liczba e « 2,71828...

y = log a* to jest to samo co _v “ log_l(,v, x > 0

Ten łogarytm aytamy jako łogarytm dziesiętny z liczby dodatniej x.

RÓWNANIA LOGARYTMICZNE przykładowe zadania Pamiętaj o wyznaczeniu dziedziny dla każdego rozwiązywanego przez Ciebie zadania.

ZADANIE 1 log_Tv = 2

Założenia: X > 0    To wynika z definicji logarytmu.

Zatem dziedziną równania jest zbiór: (0, +»)

Rozwiązanie:

log^-Y = 2 ,v = 4^:

A = 16

To wynika z definicji logarytmu log_pa = *<=> a - p*.

W tym zadaniu p = 4. <?=** = 2.

31